
【题目】已知:点P在△ABC内,且满足∠APB=∠APC(如下图),∠APB+∠BAC=180°,
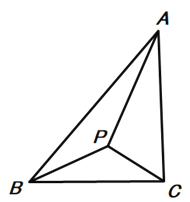
(1)求证:△PAB∽△PCA:
(2)如下图,如果∠APB=120°,∠ABC=90°求![]() 的值;
的值;
(3)如图,当∠BAC=45°,△ABC为等腰三角形时,求tan∠PBC的值.
【答案】(1)见解析;(2)4;(3)2或![]() 或1
或1
【解析】
(1)由已知和等量代换得∠PBA=∠PAC,再根据∠APB=∠APC可证明△PAB∽△PCA
(2)由△PAB∽△PCA可得![]() ,通过变形得到
,通过变形得到![]() ,再利用∠APB=120°,∠ABC=90°求出
,再利用∠APB=120°,∠ABC=90°求出![]() ,则可得出
,则可得出![]() 的值.
的值.
(3)当∠BAC=45°时,可以推出tan∠BPC=![]() ,△ABC为等腰三角形,分BA=BC,CA=CB ,AB=AC三种情况,分情况讨论即可.
,△ABC为等腰三角形,分BA=BC,CA=CB ,AB=AC三种情况,分情况讨论即可.
(1)∵∠APB+∠PBA+∠PBA=180°,∠APB+∠BAC=180°
∴∠BAC=∠PAB+∠PBA
∴∠PBA=∠PAC
∵∠APB=∠APC
∴△PAB∽△PCA
(2)
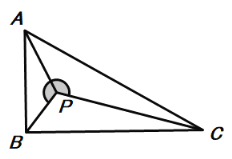
∵△PAB∽△PCA
∴![]()
∴![]()
∵∠APB=120°
∴∠BAC=60°
∵∠ABC=90°
∴![]()
∴![]()
(3)
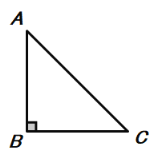
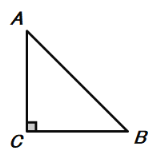
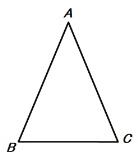
∵∠BAC=45°
∴∠APB=135°=∠APC
∴∠BPC=90°
tan∠BPC=![]()
∵∠BAC=45°,△ABC是等腰三角形
当BA=BC时,由勾股定理可得![]() ,tan∠BPC=
,tan∠BPC=![]()
当CA=CB时,由勾股定理可得![]() ,tan∠BPC=
,tan∠BPC=![]()
当AB=AC 时,tan∠BPC=![]()
综上所述,tan∠PBC=2或![]() 或1
或1


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
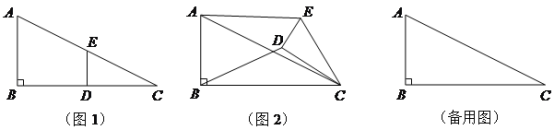
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
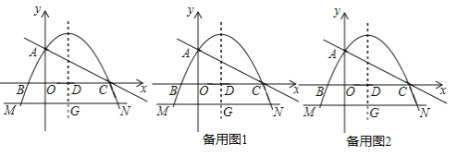
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣
x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣![]() x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.
(1)求此抛物线的解析式.
(2)求点N的坐标.
(3)过点A的直线与抛物线交于点F,当tan∠FAC=![]() 时,求点F的坐标.
时,求点F的坐标.
(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤![]() ),请直接写出S与t的函数关系式.
),请直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010﹣2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
2010 | 2011 | 2012 | 2013 | 2014 |
234 | 233 | 245 | 247 | 256 |
(1)这五年的全年空气质量优良天数的中位数是________,平均数是________;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是________年(填写年份);
(3)求这五年的全年空气质量优良天数的方差________.
查看答案和解析>>
科目:初中数学 来源: 题型:
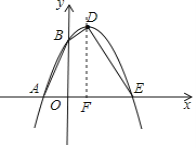
【题目】如图,已知抛物线与x轴交于点A(﹣1,0),E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求图象为下列抛物线的二次函数的表达式;
(1)抛物线y=ax2+bx+2经过点(﹣2,6)、(2,2).
(2)抛物线的顶点坐标为(3,﹣5),且抛物线经过点(0,1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com