
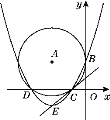
【题目】如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
(1)求经过B、C、D三点的抛物线对应的函数表达式;
(2)设抛物线的顶点为E,证明:直线CE与⊙A相切.
【答案】(1)y=![]() x2+
x2+![]() x+4;(2)详见解析.
x+4;(2)详见解析.
【解析】
(1)把B(0,4),C(﹣2,0),D(﹣8,0)代入二次函数的解析式即可得到结果;
(2)由y![]() x2
x2![]() x+4
x+4![]() (x+5)2
(x+5)2![]() ,得到顶点坐标E(﹣5,
,得到顶点坐标E(﹣5,![]() ),求得直线CE的函数解析式y
),求得直线CE的函数解析式y![]() ,在y
,在y![]() 中,令x=0,y
中,令x=0,y![]() ,得到G(0,
,得到G(0,![]() ),如图1,连接AB,AC,AG,得BG=OB﹣OG=4
),如图1,连接AB,AC,AG,得BG=OB﹣OG=4![]() ,CG
,CG![]() ,得到BG=CG,AB=AC,证得△ABG≌△ACG,得到∠ACG=∠ABG,由于⊙A与y轴相切于点B(0,4),于是得到∠ABG=90°,即可求得结论.
,得到BG=CG,AB=AC,证得△ABG≌△ACG,得到∠ACG=∠ABG,由于⊙A与y轴相切于点B(0,4),于是得到∠ABG=90°,即可求得结论.
(1)设抛物线的解析式为:y=ax2+bx+c,把B(0,4),C(﹣2,0),D(﹣8,0)代入得: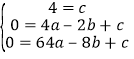 ,解得:
,解得:![]() ,∴经过B,C,D三点的抛物线的函数表达式为:y
,∴经过B,C,D三点的抛物线的函数表达式为:y![]() x2
x2![]() x+4;
x+4;
(2)∵y![]() x2
x2![]() x+4
x+4![]() (x+5)2
(x+5)2![]() ,∴E(﹣5,
,∴E(﹣5,![]() ),设直线CE的函数解析式为y=mx+n,直线CE与y轴交于点G,则
),设直线CE的函数解析式为y=mx+n,直线CE与y轴交于点G,则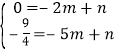 ,解得:
,解得: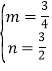 ,∴y
,∴y![]() ,在y
,在y![]() 中,令x=0,y
中,令x=0,y![]() ,∴G(0,
,∴G(0,![]() ),如图1,连接AB,AC,AG,则BG=OB﹣OG=4
),如图1,连接AB,AC,AG,则BG=OB﹣OG=4![]() ,CG
,CG![]() ,∴BG=CG,AB=AC.在△ABG与△ACG中,∵
,∴BG=CG,AB=AC.在△ABG与△ACG中,∵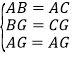 ,∴△ABG≌△ACG,∴∠ACG=∠ABG.
,∴△ABG≌△ACG,∴∠ACG=∠ABG.
∵⊙A与y轴相切于点B(0,4),∴∠ABG=90°,∴∠ACG=∠ABG=90°
∵点C在⊙A上,∴直线CE与⊙A相切.


科目:初中数学 来源: 题型:
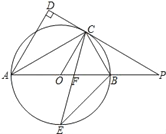
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:PC=PF;
(3)若tan∠ABC=![]() ,AB=14,求线段PC的长.
,AB=14,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
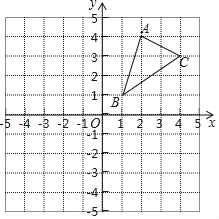
【题目】(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2.
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
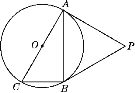
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=![]() ,∠ACB=60°,求⊙O的半径.
,∠ACB=60°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
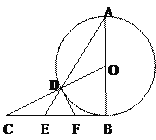
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
查看答案和解析>>
科目:初中数学 来源: 题型:
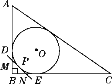
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)(x-1)2+2x(x-1)=0;
(2)x2-6x-6=0;
(3)6 000(1-x)2=4 860;
(4)(10+x)(50-x)=800;
(5)(2x-1)2=x(3x+2)-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
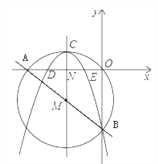
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com