练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：

    成绩/m

    1.50

    1.60

    1.65

    1.70

    1.75

    1.80

    人数

    2

    3

    2

    3

    4

    1

    则这些运动员成绩的中位数、众数分别为( )

    A. 1.70，1.75 B. 1.70，1.70

    C. 1.65，1.75 D. 1.65，1.70

    【答案】A

    【解析】

    根据中位数的定义与众数的定义，结合图表信息解答即可．

    15名运动员，按照成绩从低到高排列，第8名运动员的成绩是1.70，

    所以中位数是1.70，

    同一成绩运动员最多的是1.75，共有4人，

    所以，众数是1.75．

    因此，中位数与众数分别是1.70，1.75，

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（x+6y）（x-6y）等于（ ）

    A. x2-6y 2 B. x2-y 2 C. x2-36y 2 D. 36x2-y 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将直线y＝﹣4x+3向下平移4个单位，得到的直线解析式是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

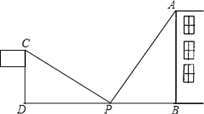
    【题目】为了测量一幢高楼高AB，在旗杆CD与最右边的高楼之间选定一点P．测得旗杆顶C视线PC与地面夹角∠DPC=38°，测楼顶A视线PA与地面夹角∠APB=52°，量得P到楼底距离PB与旗杆CD高度相等，等于8米，量得旗杆与楼之间距离为DB=33米，求楼高AB是多少米？（写出过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一组数据1，2，3，4，5的方差为2，则另一组数据11，12，13，14，15的方差为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(3z-y)2 等于（ ）

    A. 9z2-y+y2 B. 9z2-yz+y2 C. 9z2-6yz+y2 D. 3z2-6yz+y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9，这5个数据的中位数是（　　）.
    A.6
    B.7
    C.8
    D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

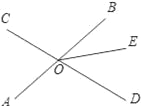
    【题目】如图，直线AB、CD相交于点O，∠AOC=72°，射线OE在∠BOD的内部，∠DOE=2∠BOE．

    （1）求∠BOE和∠AOE的度数；

    （2）若射线OF与OE互相垂直，请直接写出∠DOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

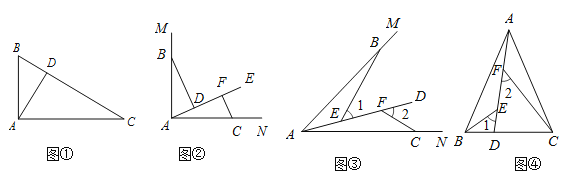
    【题目】问题情境：如图①，在直角三角形ABC中，∠BAC=，AD⊥BC于点D,可知：∠BAD=∠C（不需要证明）；

    （1）特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明：△ABD≌△CAF;

    （2）归纳证明：如图③，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证：△ABE≌△CAF;

    （3）拓展应用：如图④，在△ABC中，AB=AC，AB＞BC.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC.若△ABC的面积为15，则△ACF与△BDE的面积之和为 .

    查看答案和解析>>

    同步练习册答案