Question

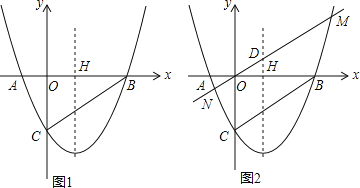
【题目】如图，已知抛物线y=x2+bx+c交x轴于点A（﹣1，0）、B（2，0），交y轴于点C，抛物线的对称轴交x轴于点H，直线y=kx（k＞0）交抛物线于点M、N（点M在N的右侧），交抛物线的对称轴于点D．

（1）求b和c的值；

（2）如图（1），若将抛物线y=x2+bx+c沿y轴方向向上平移个单位，求证：所得新抛物线图象均在直线BC的上方；

（3）如图（2），若MN∥BC．

①连接CD、BM，判断四边形CDMB是否为平行四边形，说明理由；

②以点D为圆心，DH长为半径画圆⊙D，点P、Q分别为抛物线和⊙D上的点，试求线段PQ长的最小值．

Answer 1

【答案】（1）b=﹣1，c=﹣2；（2）证明见解析；（3）①不是平行四边形，理由见解析②

【解析】

试题分析：（1）把A、B两点代入转化为方程组，即可解决问题．

（2）由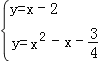消去y得到x2﹣2x+=0用判别式解决．

（3）根据两点间距离公式，利用配方法转化为二次函数最值问题即可解决．

解：（1）由题意，

解得，

所以b=﹣1，c=﹣2．

（2）∵抛物线为y=（x+1）（x﹣2）=x2﹣x﹣2，沿y轴方向向上平移个单位，

∴新抛物线为y=x2﹣x﹣，

设直线BC为y=kx+b，由题意得，

解得，

所以直线BC为y=x﹣2，

由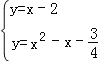消去y得到x2﹣2x+=0，

∵△=4﹣5=﹣1＜0，

∴方程组无解，抛物线与直线BC没有交点．

（3）①∵MN∥BC，

∴k=1，OM＞OB，

∴MN≠BC，

∴四边形CDMB不是平行四边形．

②设点P（m，m2﹣m﹣2），

∵点D坐标为（，），

∴PD2=（m﹣）2+（m2﹣m﹣）2

=（m﹣）2+[（m﹣）2﹣]2

=（m﹣）4﹣（m﹣）2+

=[（m﹣）2﹣]2+，

∴PD2的最小值=，

∴PD的最小值=，

∵DQ=，

∴线段PQ的最小值=．