
分析 (1)根据用3000元购买海棠、用1350元购买牵牛花,则购买的牵牛花的株数是海棠的$\frac{3}{4}$,进而得出等量关系求出即可;
(2)利用购买两种花的总株数为2000株,且总费用不能够超过3800元得出不等式求出即可.
解答 解:(1)设购买一株海棠x元,则一株牵牛花需要(x-1.2)元,根据题意可得:
$\frac{3}{4}$×$\frac{3000}{x}$=$\frac{1350}{x-1.2}$,
解得:x=3,
检验得:x=3是原方程的根,
则x-1.2=1.8.
答:购买一株海棠3元,一株牵牛花需要1.8元;
(2)设购买海棠a株,根据题意可得:
3a+1.8(2000-$\frac{a}{2}$-a)≤3800,
解得:a≤666$\frac{2}{3}$.
故我校最多可以购买666株海棠.
点评 此题主要考查了分式方程的应用以及一元一次不等式的应用,得出正确不等关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1333 | B. | 1999 | C. | 2001 | D. | 2249 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
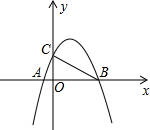 二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.
二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
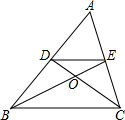 如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )
如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )| A. | 1:3 | B. | 1:9 | C. | 2:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.
在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com