
分析 (1)先计算判别式得到△=m2-4(m-2),再配方得△=(m-2)2+4,根据非负数的性质可判断△>0,然后根据判别式的意义判断根的情况.
(2)先求出方程的根,再根据条件判断△是完全平方数,于是得到关于m的方程,解出m的即可.
解答 解:(1)△=m2-4(m-2)
=m2-4m+8
=(m-2)2+4,
∵(m-2)2≥0,
∴(m-2)2+4>0,即△>0,
∴方程有两个不相等的实数根.
(2)解方程x2-mx+m-2=0得:x=$\frac{m±\sqrt{{(m-2)}^{2}+4}}{2}$,
∵方程x2-mx+m-2=0的解为整数,
∴m-2=0,
∴m=2,
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


科目:初中数学 来源: 题型:填空题
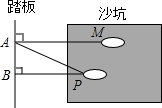 如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.
如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com