
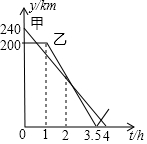
 在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号).
在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号). 分析 ①观察函数图象可知,当t=2时,两函数图象相交,结合交点代表的意义,即可得出结论①错误;②根据速度=路程÷时间分别求出甲、乙两车的速度,再根据时间=路程÷速度和可求出乙车出发1.5h时,两车相距170km,结论②正确;③根据时间=路程÷速度和可求出乙车出发2$\frac{5}{7}$h时,两车相遇,结论③正确;④结合函数图象可知当甲到C地时,乙车离开C地0.5小时,根据路程=速度×时间,即可得出结论④正确.综上即可得出结论.
解答 解:①观察函数图象可知,当t=2时,两函数图象相交,
∵C地位于A、B两地之间,
∴交点代表了两车离C地的距离相等,并不是两车相遇,结论①错误;
②甲车的速度为240÷4=60(km/h),
乙车的速度为200÷(3.5-1)=80(km/h),
∵(240+200-60-170)÷(60+80)=1.5(h),
∴乙车出发1.5h时,两车相距170km,结论②正确;
③∵(240+200-60)÷(60+80)=2$\frac{5}{7}$(h),
∴乙车出发2$\frac{5}{7}$h时,两车相遇,结论③正确;
④∵80×(4-3.5)=40(km),
∴甲车到达C地时,两车相距40km,结论④正确.
综上所述,正确的结论有:②③④.
故答案为:②③④.
点评 本题考查了一次函数的应用,根据函数图象逐一分析四条结论的正误是解题的关键.


科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 |
| 身高 | 155 | 160 | 165 | 172 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 身高 | 148 | 149 | 150 | 152 | 152 | 160 | 160 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 175 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 身高 | 145 | 160 | 150 | 152 | 160 | 154 | 160 | 166 | 167 | 168 | 160 | 169 | 173 | 174 | 175 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
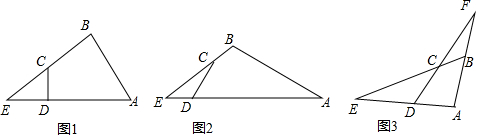
 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 两点之间线段最短 | |
| B. | 两点确定一条直线 | |
| C. | 垂线段最短 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
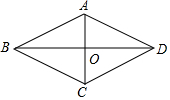 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.| A. | ③→②→①→④ | B. | ③→④→①→② | C. | ①→②→④→③ | D. | ①→④→③→② |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.
某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
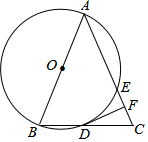 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com