
【题目】如图,在Rt△ABC中,∠ABC=90,AB=BC=![]() ,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,则BE的长是_________
,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,则BE的长是_________

【答案】![]()
【解析】
首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解.
连结CE,设BE与AC相交于点F,如图所示.
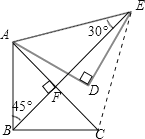
∵Rt△ABC中,AB=BC,∠ABC=90°,∴∠BCA=∠BAC=45°.
∵AB=BC=![]() ,∴AC=
,∴AC=![]() =4.
=4.
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,∴∠BAC=∠DAE=45°,AC=AE.
又∵旋转角为60°,∴∠BAD=∠CAE=60°,∴△ACE是等边三角形,∴AC=CE=AE=4.
在△ABE与△CBE中,∵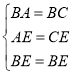 ,∴△ABE≌△CBE(SSS),∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°,∴∠BFA=180°﹣45°﹣45°=90°,∴∠AFB=∠AFE=90°.
,∴△ABE≌△CBE(SSS),∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°,∴∠BFA=180°﹣45°﹣45°=90°,∴∠AFB=∠AFE=90°.
在Rt△ABF中,由勾股定理得:BF=AF![]() 2.
2.
又在Rt△AFE中,∠AEF=30°,∠AFE=90°,FE![]() AF=2
AF=2![]() ,∴BE=BF+FE=
,∴BE=BF+FE=![]() .
.
故答案为:![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
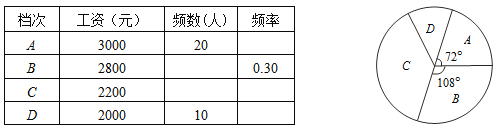
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
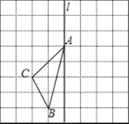
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为 ;
(3)以AC为边作与△ABC全等的三角形,则可作出 个三角形与△ABC全等;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )
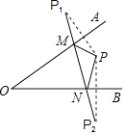
A.3cmB.4cmC.5cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
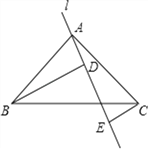
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
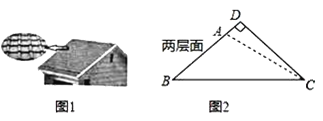
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com