
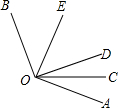
 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.分析 (1)根据角平分线的定义可得∠COD=$\frac{1}{2}$∠AOD,∠EOD=$\frac{1}{2}$∠BOD,再根据角的和差关系可得∠COE=∠EOD+∠COD=$\frac{1}{2}$∠BOA,然后再代入∠AOB的度数即可;
(2)由(1)可得∠COE=$\frac{1}{2}$∠BOA,然后再代入∠AOB的度数即可;
(3)由(1)可得∠COE=$\frac{1}{2}$∠BOA,然后再代入∠AOB=α即可.
解答 解:(1)∵OC是∠AOD的平分线,
∴∠COD=$\frac{1}{2}$∠AOD,
∵OE是∠BOD的平分线,
∴∠EOD=$\frac{1}{2}$∠BOD,
∴∠COE=∠EOD+∠COD=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOD=$\frac{1}{2}$(∠BOD+∠AOD)=$\frac{1}{2}$∠BOA,
∵∠AOB=150°,
∴∠EOC=75°;
(2)∵∠COE=$\frac{1}{2}$∠AOB,∠AOB=120°,
∴∠COE=60°,
故答案为:60°;
(3)∵∠COE=$\frac{1}{2}$∠AOB,∠AOB=α,
∴∠COE=$\frac{1}{2}α$,
故答案为:$\frac{1}{2}α$.
点评 此题主要考查了角平分线的定义,关键是掌握角平分线的定义从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.


科目:初中数学 来源: 题型:解答题
 如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答下列问题:
如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/件) | 20 | 30 |
| 售价(元/件) | 29 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
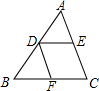 如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DF∥AC,交BC于点F.
如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DF∥AC,交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com