
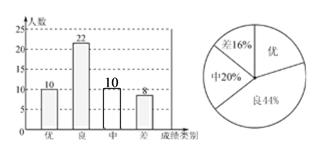
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的学习成绩达到优秀.
【答案】(1)50(名);(2)10(名);画图(3)200(名)
【解析】
试题
(1)由两幅统计图可知,成绩为差的有8人,占被抽查学生的16%,由此可计算出被抽查学生的总数;
(2)由(1)中的计算结果结合统计图中已知的数据计算出成绩为“中”的人数,参照人数即可补全条形统计图;
(3)根据(1)中计算结果可计算出被抽查学生中“优秀”所占的百分比,结合全校参考总人数为1000即可计算出所求结果.
试题解析:
(1)8÷16%=50(名),
答:本次调查共抽取了50名学生分.
(2)50×20%=10(名);补全的条形统计图如下:
(3)1000×![]() =200(名).
=200(名).
答:估计该校有200名学生的学习成绩达到优秀.


科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简)
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的![]() 满足
满足![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线,由A地到B地匀速前行,甲、乙行进的路程s与x(小时)的函数图象如图所示.(1)乙比甲晚出发___小时;(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自![]() 月
月![]() 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元 |
不超出 |
|
超出 |
|
超出 |
|
(1)若某用户![]() 月份用气量为
月份用气量为![]() ,交费多少元?
,交费多少元?
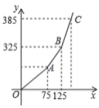
(2)调价后每月支付燃气费用![]() (单位:元)与每月用气量
(单位:元)与每月用气量![]() (单位:
(单位:![]() )的关系如图所示,求
)的关系如图所示,求![]() 与
与![]() 的解析式及
的解析式及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
(1)判断直线BE与⊙O的位置关系,并说明理由;
(2)若PB=OB=6,求弧AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.

(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=________;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
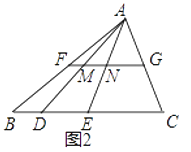
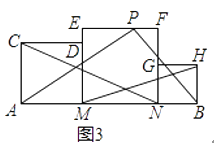
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN ,S△APB ,S△MBH的数量关系.
S△ACN=________;S△MBH=________;S△APB=________;S△ACN ,S△APB,S△MBH的数量关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB = AC,在△ABC的外部作等边三角形△ABD,E为AB的中点,连接 DE并延长交BC于点F.
(1)如图1,若∠BAC = 90°,连接CD,求证:CD平分∠ADF;
(2)如图2,过点A折叠∠CAD,使点C与点D重合,折痕AM交EF于点M,若点M正好在∠ABC的平分线上,连接BM并延长交AC于点N,课堂上两个学习小组分别得出如下两个结论:①∠BAC的度数是一个定值,为100°;②线段MN与NC一定相等.
请你选择其中一个结论,判断是否正确?若正确,给予证明:若不正确,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com