
ЁОЬтФПЁПЖЈвхЃКШчЭМ1ЃЌЕуMЃЌNАбЯпЖЮABЗжИюГЩAMЃЌMNКЭBNЃЌШєвдAMЃЌMNЃЌBNЮЊБпЕФШ§НЧаЮЪЧвЛИіжБНЧШ§НЧаЮЃЌдђГЦЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЎ

ЃЈ1ЃЉвбжЊЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌШєAM=2ЃЌMN=3ЃЌдђBN=________ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌFGЪЧжаЮЛЯпЃЌЕуDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЁнBDЃЌСЌНгADЃЌAEЗжБ№НЛFGгкЕуMЃЌNЃЌЧѓжЄЃКЕуMЃЌNЪЧЯпЖЮFGЕФЙДЙЩЗжИюЕуЃЛ
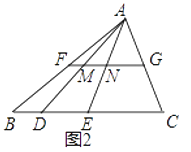
ЃЈ3ЃЉШчЭМ3ЃЌвбжЊЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌMNЃОAMЁнBNЃЌЫФБпаЮAMDCЃЌЫФБпаЮMNFEКЭЫФБпаЮNBHGОљЪЧе§ЗНаЮЃЌЕуPдкБпEFЩЯЃЌЪдЬНОПSЁїACN ЃЌSЁїAPB ЃЌSЁїMBHЕФЪ§СПЙиЯЕЃЎ
SЁїACN=________ЃЛSЁїMBH=________ЃЛSЁїAPB=________ЃЛSЁїACN ЃЌSЁїAPBЃЌSЁїMBHЕФЪ§СПЙиЯЕЪЧ________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЗжРрЬжТл:ЕБMNЮЊзюДѓЯпЖЮЪБ;ЕБBNЮЊзюДѓЯпЖЮЪБ;МДвбжЊЕФСНЬѕЯпЖЮжаНЯГЄЕФЯпЖЮMNПЩФмЮЊаББпЛђЫљЧѓЕФBNвВПЩФмЮЊаББпЃЛ
ЃЈ2ЃЉгЩвбжЊЁАFGЪЧжаЮЛЯпЁБЕУBD=2FMЃЌDE=2MNЃЌEC=2NGЃЌгЩDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЃОBDЕУГіEC2=DE2+DB2ЃЌдйЗжБ№ДњЛЛЮЊ2NGЁЂ2MNЁЂ2FMЃЌдМШЅЯЕЪ§4ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉгЩШ§НЧаЮУцЛ§ЙЋЪНЃЌЗжБ№БэЪОГіSЁїACNЁЂSЁїMBHЁЂSЁїPABЃЌЙлВь3ИіЪНзгжаЃЌГіЯжЕФAM2ЁЂBN2 ЁЂMN2ЃЌПЩЕУSЁїAPB=SЁїACN+SЁїMBH.
ЪдЬтНтЮіЃКЃЈ1ЃЉЗжСНжжЧщПіЃК
ЂйЕБMNЮЊзюДѓЯпЖЮЪБЃЌ
ЁпЕу MЁЂNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌ
ЁрBN=![]() ЃЛ
ЃЛ
ЂкЕБBNЮЊзюДѓЯпЖЮЪБЃЌ
ЁпЕуMЁЂNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌ
ЁрBN=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКBNЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЁпЕуFЁЂMЁЂNЁЂGЗжБ№ЪЧABЁЂADЁЂAEЁЂACБпЩЯЕФжаЕуЃЌ
ЁрFMЁЂMNЁЂNGЗжБ№ЪЧЁїABDЁЂЁїADEЁЂЁїAECЕФжаЮЛЯпЃЌ
ЁрBD=2FMЃЌDE=2MNЃЌEC=2NGЃЌ
ЁпЕуDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЃОBDЃЌ
ЁрEC2=DE2+DB2 ,
Ёр4NG2=4MN2+4FM2 ,
ЁрNG2=MN2+FM2 ,
ЁрЕуMЃЌNЪЧЯпЖЮFGЕФЙДЙЩЗжИюЕуЃЛ
ЂЧЁпЫФБпаЮAMDCЃЌЫФБпаЮMNFEКЭЫФБпаЮNBHGОљЪЧе§ЗНаЮЃЌ
ЁрSЁїACN= ![]() ЃЈAM+MNЃЉAC=
ЃЈAM+MNЃЉAC= ![]() ЃЈAM+MNЃЉAM=
ЃЈAM+MNЃЉAM= ![]() AM2+
AM2+ ![]() MNAMЃЌ
MNAMЃЌ
SЁїMBH= ![]() ЃЈMN+BNЃЉBH=
ЃЈMN+BNЃЉBH= ![]() ЃЈMN+BNЃЉBN=
ЃЈMN+BNЃЉBN= ![]() BN2+
BN2+ ![]() MNBNЃЌ
MNBNЃЌ
SЁїPAB= ![]() ЃЈAM+NM+BNЃЉFN=
ЃЈAM+NM+BNЃЉFN= ![]() ЃЈAM+MN+BNЃЉMN=
ЃЈAM+MN+BNЃЉMN= ![]() MN2+ /span>
MN2+ /span>![]() MNAM+
MNAM+ ![]() MNBNЃЌ
MNBNЃЌ
ЁрSЁїAPB=SЁїACN+SЁїMBH ЃЌ
ЙЪД№АИЮЊSЁїAPB=SЁїACN+SЁїMBH ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇЩњаЁУїНЋЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ЃЌГЦзїЯпЖЮ
ЃЌГЦзїЯпЖЮ![]() ЕФЁАжсЕуЁБ.ЦфжаЃЌЕБ
ЕФЁАжсЕуЁБ.ЦфжаЃЌЕБ![]() ЪБЃЌГЦ
ЪБЃЌГЦ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЁАГЄжсЕуЁБЃЛЕБ
ЕФЁАГЄжсЕуЁБЃЛЕБ![]() ЪБЃЌГЦ
ЪБЃЌГЦ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЁАЖЬжсЕуЁБ.
ЕФЁАЖЬжсЕуЁБ.
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђдк
ЃЌдђдк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жаЯпЖЮ
жаЯпЖЮ![]() ЕФЁАЖЬжсЕуЁБЪЧ______.
ЕФЁАЖЬжсЕуЁБЪЧ______.

ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсе§АыжсЩЯЃЌЧв
жсе§АыжсЩЯЃЌЧв![]() .
.

ЂйШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЁАГЄжсЕуЁБЃЌдђЕу
ЕФЁАГЄжсЕуЁБЃЌдђЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() Лђ
Лђ![]()
ЂкЕу![]() ЮЊ
ЮЊ![]() жсЩЯЕФЖЏЕуЃЌЕу
жсЩЯЕФЖЏЕуЃЌЕу![]() ЃЌ
ЃЌ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЕФЭЌВр.Шє
ЕФЭЌВр.Шє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЁАжсЕуЁБЃЌЕБЯпЖЮ
ЕФЁАжсЕуЁБЃЌЕБЯпЖЮ![]() гы
гы![]() ЕФКЭзюаЁЪБЃЌЧѓЕу
ЕФКЭзюаЁЪБЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЦРЙРОХФъМЖбЇЩњЕФбЇЯАГЩМЈзДПіЃЌвдгІЖдМДНЋЕНРДЕФжаПМзіКУНЬбЇЕїећЃЌФГжабЇГщШЁСЫВПЗжВЮМгПМЪдЕФбЇЩњЕФГЩМЈЃЌЛцжЦГЩСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉБОДЮЕїВщЙВГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉЭЈЙ§МЦЫуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃОХФъМЖЙВга1000ШЫВЮМгСЫетДЮПМЪдЃЌЧыЙРЫуИУаЃОХФъМЖЙВгаЖрЩйУћбЇЩњЕФбЇЯАГЩМЈДяЕНгХау.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШєХзЮяЯпL2ЃКy=mx2+nxЃЈmЁй0ЃЉгыХзЮяЯпL1ЃКy=ax2+bxЃЈaЁй0ЃЉЕФПЊПкДѓаЁЯрЭЌЃЌЗНЯђЯрЗДЃЌЧвХзЮяЯпL2ОЙ§L1ЕФЖЅЕуЃЌЮвУЧГЦХзЮяЯпL2ЮЊL1ЕФЁАгбКУХзЮяЯпЁБЃЎ
ЃЈ1ЃЉШєL1ЕФБэДяЪНЮЊy=x2Љ2xЃЌЧѓL1ЕФЁАгбКУХзЮяЯпЁБЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊХзЮяЯпL2ЃКy=mx2+nxЮЊL1ЃКy=ax2+bxЕФЁАгбКУХзЮяЯпЁБЃЎЧѓжЄЃКХзЮяЯпL1вВЪЧL2ЕФЁАгбКУХзЮяЯпЁБЃЛ
ЃЈ3ЃЉЦНУцЩЯгаЕуPЃЈ1ЃЌ0ЃЉЃЌQЃЈ3ЃЌ0ЃЉЃЌХзЮяЯпL2ЃКy=mx2+nxЮЊL1ЃКy=ax2ЕФЁАгбКУХзЮяЯпЁБЃЌЧвХзЮяЯпL2ЕФЖЅЕудкЕквЛЯѓЯоЃЌзнзјБъЮЊ2ЃЌЕБХзЮяЯпL2гыЯпЖЮPQУЛгаЙЋЙВЕуЪБЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЬњТЗЩЯAЃЌBСНЕуЯрОр25 kmЃЌCЃЌDЮЊСНДхзЏЃЌDAЁЭABгкЕуAЃЌCBЁЭABгкЕуBЃЌвбжЊDAЃН15 kmЃЌCBЃН10 kmЃЌЯждквЊдкЬњТЗABЩЯНЈвЛИіЭСЬиВњЦЗЪеЙКеОEЃЌЪЙЕУCЃЌDСНДхЕНEеОЕФОрРыЯрЕШЃЌдђEеОгІНЈдкРыAеОЖрЩйkmДІЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
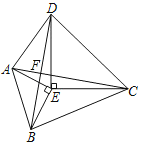
ЁОЬтФПЁПвбжЊЃКЕШбќЁїDECЃЌЁЯDECЃН90ЁуЃЌDEЃНECЃН3ЃЌвбжЊЕШбќЁїAEBЃЌЁЯAEBЃН90ЁуЃЌAEЃНBEЃН2ЃЎ
ЃЈlЃЉЧѓжЄЃКЁїDEBЁеЁїCEAЃЛ
ЃЈ2ЃЉХаЖЯBDгыACЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєЁЯDAEЃН90ЁуЃЌЧыжБНгаДГіBCЕФГЄЃЌBCЃНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌABЁЭBDЃЌsinA=![]() ЃЌНЋABCDЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЧвADЁЭxжсЃЌЕуDЕФКсзјБъЮЊ1ЃЌЕуCЕФзнзјБъЮЊ3ЃЌЧЁгавЛЬѕЫЋЧњЯпy=
ЃЌНЋABCDЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЧвADЁЭxжсЃЌЕуDЕФКсзјБъЮЊ1ЃЌЕуCЕФзнзјБъЮЊ3ЃЌЧЁгавЛЬѕЫЋЧњЯпy=![]() ЃЈkЃО0ЃЉЭЌЪБОЙ§BЁЂDСНЕуЃЌдђЕуBЕФзјБъЪЧ_____ЃЎ
ЃЈkЃО0ЃЉЭЌЪБОЙ§BЁЂDСНЕуЃЌдђЕуBЕФзјБъЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЯвCDгыжБОЖABЯрНЛгкЕуFЃЎЕуEдкЁбOЭтЃЌзїжБЯпAEЃЌЧвЁЯEACЃНЁЯDЃЎ
(1)ЧѓжЄЃКжБЯпAEЪЧЁбOЕФЧаЯпЃЎ
(2)ШєЁЯBACЃН30ЁуЃЌBCЃН4ЃЌcosЁЯBADЃН![]() ЃЌCFЃН
ЃЌCFЃН![]() ЃЌЧѓBFЕФГЄЃЎ
ЃЌЧѓBFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊвЛДЮКЏЪ§
жаЃЌвбжЊвЛДЮКЏЪ§![]() ЃН
ЃН![]() ЕФЭМЯѓОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌгыЗДБШР§КЏЪ§
ЕФЭМЯѓОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌгыЗДБШР§КЏЪ§![]() ЃН
ЃН![]() ЃЈ
ЃЈ![]() ЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈ2ЃЌ1ЃЉЃЎ
ЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈ2ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕКЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЕФжЕКЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНсКЯЭМЯѓжБНгаДГіЃКЕБ![]() ЃО0ЪБЃЌВЛЕШЪН
ЃО0ЪБЃЌВЛЕШЪН![]() ЃО
ЃО![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com