
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
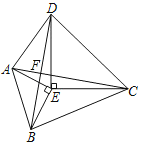
【答案】(1)详见解析;(2)BD⊥AC,BD=AC,理由详见解析;(3)![]() .
.
【解析】
(1)证明∠AEC=∠BED,根据SAS可得△DEB≌△CEA;
(2)证明△DEB≌△CEA,得出∠ACE=∠BDE,AC=BD,由三角形内角和定理得∠CFB=∠DEC=90°,得出AC⊥BD;
(3)由AC⊥BD,可得AB2+CD2=AD2+BC2,求出AB2,CD2,AD2即可得出答案.
解:(1)证明:∵∠AEB+∠AED=∠DEC+∠AED,
∴∠AEC=∠BED,
在△DEB和△CEA中,
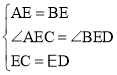 ,
,
∴△DEB≌△CEA(SAS),
(2)解:BD⊥AC,BD=AC,理由如下:
∵△DEB≌△CEA,
∴∠ACE=∠BDE,AC=BD,
∵∠AND=∠CNE,如图所示:
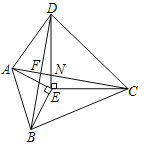
∴由三角形内角和定理得:∠CFB=∠DEC=90°,
∴AC⊥BD.
(3)解:∵AC⊥BD,
∴DF2+CF2=DC2,AF2+BF2=AB2,
∴AB2+CD2=DF2+CF2+AF2+BF2=AD2+BC2,
∵∠DAE=90°,DE=3,AE=2,
∴AD2=DE2﹣AE2=9﹣4=5,
∵∠AEB=90°,AE=BE=2.
∴AB2=4+4=8,
∵∠DEC=90°,DE=EC=3,
∴DC2=9+9=18,
∴BC2=AB2+CD2﹣AD2=8+18﹣5=21,
∴BC=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自![]() 月
月![]() 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元 |
不超出 |
|
超出 |
|
超出 |
|
(1)若某用户![]() 月份用气量为
月份用气量为![]() ,交费多少元?
,交费多少元?
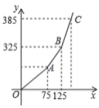
(2)调价后每月支付燃气费用![]() (单位:元)与每月用气量
(单位:元)与每月用气量![]() (单位:
(单位:![]() )的关系如图所示,求
)的关系如图所示,求![]() 与
与![]() 的解析式及
的解析式及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.

(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=________;
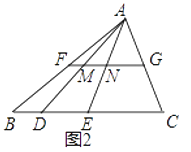
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
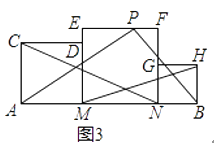
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN ,S△APB ,S△MBH的数量关系.
S△ACN=________;S△MBH=________;S△APB=________;S△ACN ,S△APB,S△MBH的数量关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
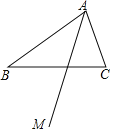
【题目】如图,在△ABC中,射线AM平分∠BAC.
(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG;
(2)在(1)条件下,∠BAC和∠BGC有何数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,作
的中点,作![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)若![]() ,求线段
,求线段![]() 的长;
的长;
(2)当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+2mx-m2+![]() 的顶点为P.
的顶点为P.
(1)求证:不论m取何值,点P始终在同一个反比例函数图象上?
(2)若抛物线与x轴交于A、B两点,当m为何值时,线段AB长等于8?
(3)该抛物线上是否存在一点Q,使得△OPQ是以点P为顶点的等腰直角三角形?若不存在,请说明理由;若存在,请求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com