
【题目】如图,在△ABC中,射线AM平分∠BAC.
(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG;
(2)在(1)条件下,∠BAC和∠BGC有何数量关系?并证明你的结论.
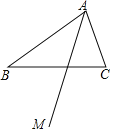
【答案】(1)详见解析;(2)∠BAC+∠BGC=180°,证明详见解析.
【解析】
(1)作线段BC的垂直平分线即可;
(2)在AB上截取AD=AC,连接DG.首先证明△DAG≌△CAG(SAS),推出∠ABG+∠ACG=180°,利用四边形内角和定理即可解决问题.
解:(1)线段BC的中垂线EG如图所示:
(2)结论:∠BAC+∠BGC=180°.
理由:在AB上截取AD=AC,连接DG.
∵AM平分∠BAC,
∴∠DAG=∠CAG,
在△DAG和△CAG中
∵
∴△DAG≌△CAG(SAS),
∴∠ADG=∠ACG,DG=CG,
∵G在BC的垂直平分线上,
∴BG=CG,
∴BG=DG,
∴∠ABG=∠BDG,
∵∠BDG+∠ADG=180°,
∴∠ABG+∠ACG=180°,
∵∠ABG+∠BGC+∠ACG+∠BAC=360°,
∴∠BAC+∠BGC=180°.


科目:初中数学 来源: 题型:
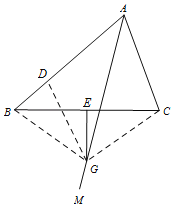
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若抛物线L2:y=mx2+nx(m≠0)与抛物线L1:y=ax2+bx(a≠0)的开口大小相同,方向相反,且抛物线L2经过L1的顶点,我们称抛物线L2为L1的“友好抛物线”.
(1)若L1的表达式为y=x2﹣2x,求L1的“友好抛物线”的表达式;
(2)已知抛物线L2:y=mx2+nx为L1:y=ax2+bx的“友好抛物线”.求证:抛物线L1也是L2的“友好抛物线”;
(3)平面上有点P(1,0),Q(3,0),抛物线L2:y=mx2+nx为L1:y=ax2的“友好抛物线”,且抛物线L2的顶点在第一象限,纵坐标为2,当抛物线L2与线段PQ没有公共点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
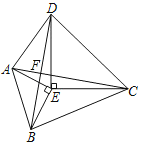
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥BD,sinA=![]() ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=![]() (k>0)同时经过B、D两点,则点B的坐标是_____.
(k>0)同时经过B、D两点,则点B的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
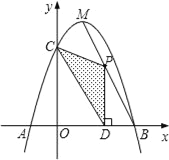
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=![]() ,CF=
,CF=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学的课余生活,某学校将举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是________”的问卷调查,要求学生只能从“A(绿博园),B(人民公园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

回答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校共有3 600名学生,试估计该校去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(c≠4a),其图象L经过点A(-2,0).
(1)求证:b2-4ac>0;
(2)若点B(-![]() ,b+3)在图象L上,求b的值;
,b+3)在图象L上,求b的值;
(3)在(2)的条件下,若图象L的对称轴为直线x=3,且经过点C(6,-8),点D(0,n)在y轴负半轴上,直线BD与OC相交于点E,当△ODE为等腰三角形时,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com