
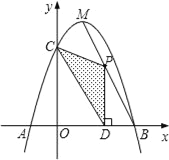
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cгыxжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌЧвЕуBгыЕуCЕФзјБъЗжБ№ЮЊBЃЈ3ЃЌ0ЃЉЃЎCЃЈ0ЃЌ3ЃЉЃЌЕуMЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮMBЩЯвЛИіЖЏЕуЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЎШєOD=mЃЌЁїPCDЕФУцЛ§ЮЊSЃЌЪдХаЖЯSгазюДѓжЕЛђзюаЁжЕЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкMBЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPCDЮЊжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉНтЮіЪНЮЊy=Љx2+2x+3ЃЛЃЈ2ЃЉЕБm=![]() ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ ЃЈ3ЃЉДцдкЃЌPЕузјБъЮЊЃЈ
ЃЛ ЃЈ3ЃЉДцдкЃЌPЕузјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈЉ3+3
ЃЌ3ЃЉЛђЃЈЉ3+3![]() ЃЌ12Љ6
ЃЌ12Љ6![]() ЃЉЪБЃЌЁїPCDЮЊжБНЧШ§НЧаЮЃЎ
ЃЉЪБЃЌЁїPCDЮЊжБНЧШ§НЧаЮЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбBЕуКЭCЕузјБъДњШыy=Љx2+bx+cЕУЕНЙигкbЁЂcЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщЧѓГіbЁЂcМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉАбЃЈ1ЃЉжаЕФвЛАуЪНХфГЩЖЅЕуЪНПЩЕУЕНMЃЈ1ЃЌ4ЃЉЃЌЩшжБЯпBMЕФНтЮіЪНЮЊy=kx+nЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBMЕФНтЮіЪНЃЌдђPЃЈmЃЌЉ2m+6ЃЉЃЈ1ЁмmЃМ3ЃЉЃЌгкЪЧИљОнШ§НЧаЮУцЛ§ЙЋЪНЕУЕНS=Љm2+3mЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЬжТлЃКЁЯPDCВЛПЩФмЮЊ90ЁуЃЛЕБЁЯDPC=90ЁуЪБЃЌвзЕУЉ2m+6=3ЃЌНтЗНГЬЧѓГіmМДПЩЕУЕНДЫЪБPЕузјБъЃЛЕБЁЯPCD=90ЁуЪБЃЌРћгУЙДЙЩЖЈРэЕУЕНКЭСНЕуМфЕФОрРыЙЋЪНЕУЕНm2+ЃЈЉ2m+3ЃЉ2+32+m2=ЃЈЉ2m+6ЃЉ2ЃЌ
ШЛКѓНтЗНГЬЧѓГіТњзуЬѕМўЕФmЕФжЕМДПЩЕУЕНДЫЪБPЕузјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉАбBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉДњШыy=Љx2+bx+cЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯпНтЮіЪНЮЊy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉSгазюДѓжЕЃЎРэгЩШчЯТЃК
Ёпy=Љx2+2x+3=ЉЃЈxЉ1ЃЉ2+4ЃЌ
ЁрMЃЈ1ЃЌ4ЃЉЃЌ
ЩшжБЯпBMЕФНтЮіЪНЮЊy=kx+nЃЌ
АбBЃЈ3ЃЌ0ЃЉЃЌMЃЈ1ЃЌ4ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBMЕФНтЮіЪНЮЊy=Љ2x+6ЃЌ
ЁпOD=mЃЌ
ЁрPЃЈmЃЌЉ2m+6ЃЉЃЈ1ЁмmЃМ3ЃЉЃЌ
ЁрS=![]() mЃЈЉ2m+6ЃЉ=Љm2+3m=ЉЃЈmЉ
mЃЈЉ2m+6ЃЉ=Љm2+3m=ЉЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
Ёп1ЁмmЃМ3ЃЌ
ЁрЕБm=![]() ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкЃЎ
ЁЯPDCВЛПЩФмЮЊ90ЁуЃЛ
ЕБЁЯDPC=90ЁуЪБЃЌдђPD=OC=3ЃЌМДЉ2m+6=3ЃЌНтЕУm=![]() ЃЌДЫЪБPЕузјБъЮЊЃЈ
ЃЌДЫЪБPЕузјБъЮЊЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ
ЕБЁЯPCD=90ЁуЪБЃЌдђPC2+CD2=PD2ЃЌМДm2+ЃЈЉ2m+3ЃЉ2+32+m2=ЃЈЉ2m+6ЃЉ2ЃЌ
ећРэЕУm2+6mЉ9=0ЃЌНтЕУm1=Љ3Љ3![]() ЃЈЩсШЅЃЉЃЌm2=Љ3+3
ЃЈЩсШЅЃЉЃЌm2=Љ3+3![]() ЃЌ
ЃЌ
ЕБm=Љ3+3![]() ЪБЃЌy=Љ2m+6=6Љ6
ЪБЃЌy=Љ2m+6=6Љ6![]() +6=12Љ6
+6=12Љ6![]() ЃЌДЫЪБPЕузјБъЮЊЃЈЉ3+3
ЃЌДЫЪБPЕузјБъЮЊЃЈЉ3+3![]() ЃЌ12Љ6
ЃЌ12Љ6![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЕБPЕузјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈЉ3+3
ЃЌ3ЃЉЛђЃЈЉ3+3![]() ЃЌ12Љ6
ЃЌ12Љ6![]() ЃЉЪБЃЌЁїPCDЮЊжБНЧШ§НЧаЮЃЎ
ЃЉЪБЃЌЁїPCDЮЊжБНЧШ§НЧаЮЃЎ


 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
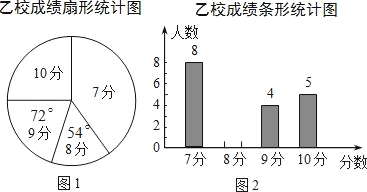
ЁОЬтФПЁПЃЈ10ЗжЃЉМзЁЂввСНаЃВЮМгЪаНЬг§ОжОйАьЕФГѕжаЩњгЂгяПкгяОКШќЃЌСНаЃВЮШќШЫЪ§ЯрЕШЃЎБШШќНсЪјКѓЃЌЗЂЯжбЇЩњГЩМЈЗжБ№ЮЊ7ЗжЁЂ8ЗжЁЂ9ЗжЁЂ10ЗжЃЈТњЗжЮЊ10ЗжЃЉЃЎвРОнЭГМЦЪ§ОнЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМБэЃЎ
ЗжЪ§ | 7Зж | 8Зж | 9Зж | 10Зж |
ШЫЪ§ | 11 | 0 | ЁЁ ЁЁ | 8 |
ЃЈ1ЃЉЧыНЋМзаЃГЩМЈЭГМЦБэКЭЭМ2ЕФЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉОМЦЫуЃЌвваЃЕФЦНОљЗжЪЧ8.3ЗжЃЌжаЮЛЪ§ЪЧ8ЗжЃЌЧыаДГіМзаЃЕФЦНОљЗжЁЂжаЮЛЪ§ЃЛВЂДгЦНОљЗжКЭжаЮЛЪ§ЕФНЧЖШЗжЮіФФИібЇаЃГЩМЈНЯКУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП10mЃН2ЃЌ10nЃН3ЃЌдђ103m+2nЉ1ЕФжЕЮЊ(ЁЁЁЁ)
A. 7B. 7.1C. 7.2D. 7.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌЪЧецУќЬтЕФЪЧЃЈ ЃЉ
A.вЛИіНЧЕФгрНЧДѓгкетИіНЧ
B.СкВЙНЧвЛЖЈЛЅВЙ
C.ЯрЕШЕФНЧЪЧЖдЖЅНЧ
D.гаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпДЙжБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіЖрБпаЮЕФФкНЧКЭЪЧЫќЕФЭтНЧКЭЕФ2БЖЃЌФЧУДетИіЖрБпаЮЕФБпЪ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСадЫЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.ЉaЃЈaЉbЃЉ=Љa2Љab
B.ЃЈ2abЃЉ2+a2b=4ab
C.2ab3a=6a2b
D.ЃЈaЉ1ЃЉЃЈ1ЉaЃЉ=a2Љ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊПѓШЊЫЎУПЦП3дЊЃЌЧв3ИіПеПѓШЊЫЎЦППЩвдЛЛвЛЦППѓШЊЫЎЃЌЯжгаМИИібЇЩњДј15дЊЧЎШЅТђПѓШЊЫЎКШЃЌЫћУЧзюЖрПЩвдКШПѓШЊЫЎЕФЦПЪ§ЮЊ( )
A. 5B. 8C. 7D. 6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгке§БШР§КЏЪ§y=mx|m|Љ1 ЃЌ ШєyЕФжЕЫцxЕФжЕдіДѓЖјМѕаЁЃЌдђmЕФжЕЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЕШЪНДгзѓЕНгвЕФБфаЮЪЧвђЪНЗжНтЕФЪЧЃЈЁЁЁЁЃЉ
A. 2xЃЈx+3ЃЉЃН2x2+6x B. 24xy2ЃН3x8y2
C. x2+2xy+y2+1ЃНЃЈx+yЃЉ2+1 D. x2Љy2ЃНЃЈx+yЃЉЃЈxЉyЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com