
【题目】已知二次函数y=ax2+bx+c(c≠4a),其图象L经过点A(-2,0).
(1)求证:b2-4ac>0;
(2)若点B(-![]() ,b+3)在图象L上,求b的值;
,b+3)在图象L上,求b的值;
(3)在(2)的条件下,若图象L的对称轴为直线x=3,且经过点C(6,-8),点D(0,n)在y轴负半轴上,直线BD与OC相交于点E,当△ODE为等腰三角形时,求n的值.
【答案】(1)证明见解析;(2)-3;(3)![]() 或
或![]()
【解析】试题分析:(1)将点A坐标代入函数解析式中,得b=2a+ ![]() c,再代入b2-4ac中得,b2-4ac=(2a-
c,再代入b2-4ac中得,b2-4ac=(2a-![]() c)2,由c≠4a得2a-
c)2,由c≠4a得2a-![]() c≠0,所以(2a-
c≠0,所以(2a-![]() c)2>0,即b2-4ac>0. (2)将点B的坐标代入函数解析式中得:
c)2>0,即b2-4ac>0. (2)将点B的坐标代入函数解析式中得: ![]() ,由4a-2b+c=0,所以b+3=0,解得b=-3;(3)由题意,得
,由4a-2b+c=0,所以b+3=0,解得b=-3;(3)由题意,得![]() ,且36a-18+c=-8,解得a=
,且36a-18+c=-8,解得a=![]() ,c=-8.所以图象L的解析式为y=
,c=-8.所以图象L的解析式为y=![]() x2-3x-8. 设OC与对称轴交于点Q,图象L与y轴相交于点P,则Q(3,-4),P(0,-8),OQ=PQ=5.分两种情况:①当OD=OE时,②当EO=ED时,讨论求值即可;
x2-3x-8. 设OC与对称轴交于点Q,图象L与y轴相交于点P,则Q(3,-4),P(0,-8),OQ=PQ=5.分两种情况:①当OD=OE时,②当EO=ED时,讨论求值即可;
试题解析:
(1)证明:
由题意,得4a-2b+c=0,
∴b=2a+![]() c.
c.
∴b2-4ac=(2a+![]() c)2-4ac=(2a-
c)2-4ac=(2a-![]() c)2.
c)2.
∵c≠4a,
∴2a-![]() c≠0,
c≠0,
∴(2a-![]() c)2>0,即b2-4ac>0.
c)2>0,即b2-4ac>0.
(2)解:∵点B(-![]() ,b+3)在图象L上,
,b+3)在图象L上,
∴![]() ,整理,得
,整理,得![]() .
.
∵4a-2b+c=0,
∴b+3=0,解得b=-3.
(3)解:由题意,得![]() ,且36a-18+c=-8,解得a=
,且36a-18+c=-8,解得a=![]() ,c=-8.
,c=-8.
∴图象L的解析式为y=![]() x2-3x-8.
x2-3x-8.
设OC与对称轴交于点Q,图象L与y轴相交于点P,
则Q(3,-4),P(0,-8),OQ=PQ=5.
分两种情况:
①当OD=OE时,如图1,
过点Q作直线MQ∥DB,交y轴于点M,交x轴于点H,
则![]() ,
,
∴OM=OQ=5.
∴点M的坐标为(0,-5).
设直线MQ的解析式为![]() .
.
∴![]() ,解得
,解得![]() .
.
∴MQ的解析式为![]() .易得点H(15,0).
.易得点H(15,0).
又∵MH∥DB, ![]() .
.
即![]() ,
,
∴![]() .
.
②当EO=ED时,如图2,
∵OQ=PQ,
∴![]() 1=
1=![]() 2,又EO=ED,
2,又EO=ED,
∴![]() 1=
1=![]() 3.
3.
∴![]() 2=
2=![]() 3,
3,
∴PQ∥DB.
设直线PQ交于点N,其函数表达式为![]()
∴![]() ,解得
,解得![]() .
.
∴PQ的解析式为![]() .
.
∴点N的坐标为(6,0).
∵PN∥DB,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.

综上所述,当△ODE是等腰三角形时,n的值为![]() 或
或![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的盒中装着大小、外形、质地一样的红色、黑色、白色的乒乓球共20个,通过多次摸球实验后发现其中摸到红色、黑色球的概率稳定在5%和15%,则盒子中白色球的个数很可能是__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冥王星围绕太阳公转的轨道半径长度约为5900000000千米,5900000000用科学记数法表示是( )
A. 5.9×1010B. 5.9×109C. 59×108D. 0.59×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的命题个数为( )
①所有的等腰三角形都相似;
②有一对锐角相等的两个直角三角形相似;
③所有的正方形都相似;
④四个角对应相等的两个梯形相似.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF. 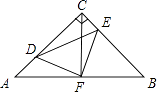
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(﹣1,y1),(2,y2),(﹣3,y3),则你认为y1 , y2 , y3的大小关系应为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com