
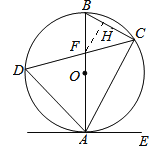
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=![]() ,CF=
,CF=![]() ,求BF的长.
,求BF的长.

【答案】(1)见解析;(2)3.
【解析】
试题(1)、根据直径所对的圆周角为直角得出∠BCA=90°,从而得出∠B+∠BAC=90°,根据∠B=∠D,∠EAC=∠D得出∠B=∠EAC,从而利用等量代换得出∠BAE=90°,得出切线;(2)、过点F作FH⊥BC于点H,根据同弧所对的圆周角相等得出∠BAD=∠BCD,根据CF的长度求出CH的长度,然后求出BH的长度,然后根据∠B=60°以及Rt△BFH的三角函数求出BF的长度.
试题解析:解:(1)证明:∵AB是⊙O的直径, ∴∠BCA=90°, ∴∠B+∠BAC=90°,
∵∠D=∠B,∠EAC=∠D, ∴∠EAC=∠B,∴∠EAC+∠BAC=90°,即∠BAE=90°,
∴BA⊥AE, ∵BA过O, ∴直线AE是⊙O的切线.
(2)解:如图,作FH⊥BC于点H,
∵∠BAD=∠BCD,cos∠BAD=![]() , ∴cos∠BCD =
, ∴cos∠BCD =![]() ,
,
在Rt△CFH中,∵CF=![]() ∴CH=CF·cos∠BCD=
∴CH=CF·cos∠BCD=![]() ×
×![]() =
=![]() ,
,
∵BC=4, ∴BH=BC-CH=4-![]() =
=![]() ,
,
∵AB是⊙O的直径, ∴∠BCA=90°, ∵∠BAC=30°, ∴∠B=60°,
∴BF=![]() =
=![]() =3.
=3.


科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简)
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的![]() 满足
满足![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.

(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=________;
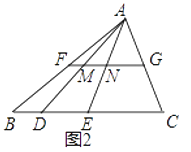
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
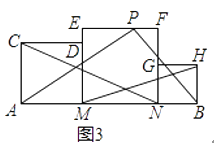
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN ,S△APB ,S△MBH的数量关系.
S△ACN=________;S△MBH=________;S△APB=________;S△ACN ,S△APB,S△MBH的数量关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
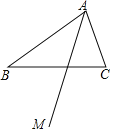
【题目】如图,在△ABC中,射线AM平分∠BAC.
(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG;
(2)在(1)条件下,∠BAC和∠BGC有何数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,作
的中点,作![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)若![]() ,求线段
,求线段![]() 的长;
的长;
(2)当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB = AC,在△ABC的外部作等边三角形△ABD,E为AB的中点,连接 DE并延长交BC于点F.
(1)如图1,若∠BAC = 90°,连接CD,求证:CD平分∠ADF;
(2)如图2,过点A折叠∠CAD,使点C与点D重合,折痕AM交EF于点M,若点M正好在∠ABC的平分线上,连接BM并延长交AC于点N,课堂上两个学习小组分别得出如下两个结论:①∠BAC的度数是一个定值,为100°;②线段MN与NC一定相等.
请你选择其中一个结论,判断是否正确?若正确,给予证明:若不正确,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
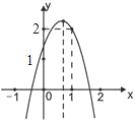
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,且关于x的方程![]() 的解为整数,则满足条件的所有整数a的和是( )
的解为整数,则满足条件的所有整数a的和是( )
A.﹣2B.﹣1C.1D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com