
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,作
的中点,作![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)若![]() ,求线段
,求线段![]() 的长;
的长;
(2)当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)满足条件的
;(3)满足条件的![]() 的长为
的长为![]() ,
,![]() .
.
【解析】
(1)连接BE,点D是AB中点且DE⊥AB,BE=AE,利用线段垂直平分线的性质和含30度角的直角三角形即可求出线段CE的长;
(2)连接BE,则AE=BE=6-y,由勾股定理得BC2+CE2=BE2,即x2+y2=(6-y)2,整理即可得出y关于x的函数解析式![]() ;
;
(3)此题有两种情况:①是当点E在线段AC上时,由(2)得![]() ,解得x即可;②是当点E在AC延长线上时,AE=BE=7,由勾股定理得BC2+CE2=BE2即x2+12=72.解得x即可.
,解得x即可;②是当点E在AC延长线上时,AE=BE=7,由勾股定理得BC2+CE2=BE2即x2+12=72.解得x即可.
(1)如图,连接![]() ,
,
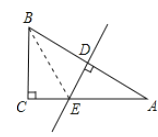
∵点![]() 是
是![]() 中点且
中点且![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴∠ABC=90°-∠A=60°,![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,AC=AE+CE,
,AC=AE+CE,
∴![]() ,
,
(2)连接![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,即
,即![]() ,
,
解得![]()
(3)①当点![]() 在线段
在线段![]() 上时,由(2)得
上时,由(2)得![]() ,
,
解得![]() (负值已舍)
(负值已舍)
②当点![]() 在
在![]() 延长线上时,
延长线上时,
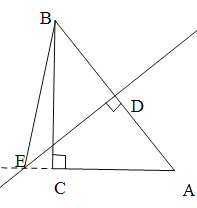
![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,即
,即![]() .
.
解得![]() (负值已舍)
(负值已舍)
综上所述,满足条件的![]() 的长为
的长为![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
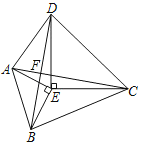
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
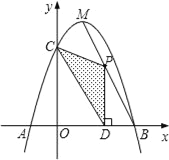
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=![]() ,CF=
,CF=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆70周年前夕,网店销售 三种规格的手摇小国旗,其部分相关信息如下表:
型号 | 规格(mm) | 批发价(元/面) | 建议零售价(元/面) |
大号 | 45x30 | 2.00 | |
中号 | 28x20 | 1.50 | |
小号 | 22x14 |
已知大号小国旗比中号的批发价贵0.3元,小号小国旗比中号的批发价便宜0.1元某小商品零售商店,第一次用 380元购进了一批大号小国旗,紧接着又用780元购进了第二 批中号小国旗,第二批的数量是第一批的3倍.
(1)求三种型号小国旗的批发价分别是多少元?
(2)该商店很快又购进了第三批小号小国旗1200面.如果三批小国旗全部按网店建议零 售价销售完后,该零售商店获利不少于1980 元,那么小号小国旗的建议零售价至少 为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学的课余生活,某学校将举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是________”的问卷调查,要求学生只能从“A(绿博园),B(人民公园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

回答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校共有3 600名学生,试估计该校去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=______°;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.

(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com