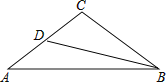
【题目】如图，△ABC中，CA=CB，∠ACB=108°，BD平分∠ABC交AC于D，求证：AB=AD+BC.
【答案】证明见解析.
【解析】
证明线段的和差倍分问题常用截长补短的方法．在线段AB上截取BE=BC，连接DE．则只需证明AD=AE即可．结合角度证明∠ADE=∠AED．
证明：在线段BA上截取BE=BC，连接DE．
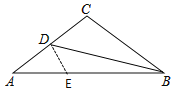
∵BD平分∠ABC，
∴∠ABD=∠EBD=
∠ABC．
在△CBD和△EBD中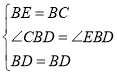
，
∴△CBD≌△EBD（SAS），
∴∠BED=∠ACB=108°，∠CDB=∠EDB．
又∵AB=AC，∠ACB=108°，∠CAB=∠ABC=×（180°-108°）=36°，
∴∠CBD=∠EBD=18°．
∴∠CDB=∠EDB=180°-18°-108°=54°．
∴∠ADE=180°-∠CDB-∠EDB=180°-54°-54°=72°．
∴∠DEA=180°-∠DEB=180°-108°=72°．
∴∠ADE=∠AED．
∴AD=AE．
∴AB=BE+EA=CB+AD．
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC和△ADE分别是以BC，DE为底边且顶角相等的等腰三角形，点D在线段BC上，AF平分DE交BC于点F，连接BE，EF．
（1）CD与BE相等？若相等，请证明；若不相等，请说明理由；
（2）若∠BAC=90°，求证：BF2+CD2=FD2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，点
是斜边
的中点，作
，交直线
于点
.
（1）若
，求线段
的长；
（2）当点在线段上时，设
，
，求
关于
的函数解析式，并写出定义域；
（3）若
，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CA⊥AB，垂足为点A，AB＝10，AC＝5，射线BM⊥AB，垂足为点B，一动点E从A点出发以2厘米秒的速度沿射线AN包括点A）运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED＝CB，当点E运动_____秒时，△DEB与△BCA全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,二次函数y=ax2+bx+c（a≠0）的图象经过点（1,2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0.1＜x2＜2.下列结论：4a+2b+c＜0；2a+b＜0；b2+8a＞4ac；
a＜﹣1；其中结论正确的有（ ）
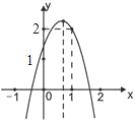
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B＝90°，∠A＝30°，AC＝2．将△ABC绕点C顺时针旋转120°得△A′B′C．
（1）求作：△A′B′C；
（2）求点B旋转经过的路径长；
（3）求线段BB′的长；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝－x2＋2mx－m2＋
的顶点为P．
（1）求证：不论m取何值，点P始终在同一个反比例函数图象上？
（2）若抛物线与x轴交于A、B两点，当m为何值时，线段AB长等于8？
（3）该抛物线上是否存在一点Q，使得△OPQ是以点P为顶点的等腰直角三角形？若不存在，请说明理由；若存在，请求出m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D为边AB上一点，CD绕点D顺时针旋转90°至DE，CE交AB于点G．已知AD＝8，BG＝6，点F是AE的中点，连接DF，求线段DF的长___．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
