
【题目】已知抛物线y=-x2+2mx-m2+![]() 的顶点为P.
的顶点为P.
(1)求证:不论m取何值,点P始终在同一个反比例函数图象上?
(2)若抛物线与x轴交于A、B两点,当m为何值时,线段AB长等于8?
(3)该抛物线上是否存在一点Q,使得△OPQ是以点P为顶点的等腰直角三角形?若不存在,请说明理由;若存在,请求出m的值.
【答案】(1)答案见解析;(2)![]() ;(3)±1.
;(3)±1.
【解析】
(1)先求出二次函数的顶点坐标,根据反比例函数性质即可得出结论;(2)把y=0代入函数解析式得到关于m的一元二次方程,再由m>0,即可求解;(3)分m>0,m<0,两种情况讨论即可.
本题解析:
(1)证明:∵y=-x2+2mx-m2+![]() ,∴y=-(x-m)2+
,∴y=-(x-m)2+![]() ,∴P(m,
,∴P(m,![]() ).
).
∵m×![]() =1,∴点P始终在
=1,∴点P始终在![]() 图象上
图象上
(2)把y=0代入y=-x2+2mx-m2+![]() 中
中
-x2+2mx-m2+![]() =0
=0
(x-m)2=![]()
当m>0时,x=m±![]() ,∴AB=
,∴AB=![]() ,∴m=
,∴m=![]() .
.
(3)①当m>0,∠OPQ=90°时
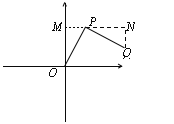
如图,可证△OPM≌△PQN.
∵P(m,![]() ),∴Q(m+
),∴Q(m+![]() ,
,![]() -m)(注:抛物线开口向下,只有这一种情况)
-m)(注:抛物线开口向下,只有这一种情况)
∴![]() -m=-(m+
-m=-(m+![]() -m)2+
-m)2+![]() ,解得m=1.
,解得m=1.
②当m<0,∠OPQ=90°时
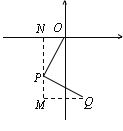
∵P(m,![]() ),∴Q(m-
),∴Q(m-![]() ,
,![]() +m) (注:抛物线开口向下,只有这一种情况)
+m) (注:抛物线开口向下,只有这一种情况)
∴![]() +m=-(m-
+m=-(m-![]() -m)2+
-m)2+![]() ,解得m=-1.
,解得m=-1.
综上所述:m的值为±1.


科目:初中数学 来源: 题型:
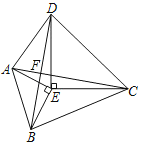
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学的课余生活,某学校将举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是________”的问卷调查,要求学生只能从“A(绿博园),B(人民公园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

回答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校共有3 600名学生,试估计该校去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() =
=![]() 的图象经过点A(1,0),与反比例函数
的图象经过点A(1,0),与反比例函数![]() =
=![]() (
(![]() >0)的图象相交于点B(2,1).
>0)的图象相交于点B(2,1).
(1)求![]() 的值和一次函数的解析式;
的值和一次函数的解析式;
(2)结合图象直接写出:当![]() >0时,不等式
>0时,不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(c≠4a),其图象L经过点A(-2,0).
(1)求证:b2-4ac>0;
(2)若点B(-![]() ,b+3)在图象L上,求b的值;
,b+3)在图象L上,求b的值;
(3)在(2)的条件下,若图象L的对称轴为直线x=3,且经过点C(6,-8),点D(0,n)在y轴负半轴上,直线BD与OC相交于点E,当△ODE为等腰三角形时,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=______°;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.

(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com