
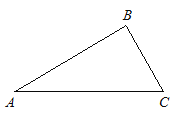
【题目】如图,在△ABC中,∠B=90°,∠A=30°,AC=2.将△ABC绕点C顺时针旋转120°得△A′B′C.
(1)求作:△A′B′C;
(2)求点B旋转经过的路径长;
(3)求线段BB′的长;
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆70周年前夕,网店销售 三种规格的手摇小国旗,其部分相关信息如下表:
型号 | 规格(mm) | 批发价(元/面) | 建议零售价(元/面) |
大号 | 45x30 | 2.00 | |
中号 | 28x20 | 1.50 | |
小号 | 22x14 |
已知大号小国旗比中号的批发价贵0.3元,小号小国旗比中号的批发价便宜0.1元某小商品零售商店,第一次用 380元购进了一批大号小国旗,紧接着又用780元购进了第二 批中号小国旗,第二批的数量是第一批的3倍.
(1)求三种型号小国旗的批发价分别是多少元?
(2)该商店很快又购进了第三批小号小国旗1200面.如果三批小国旗全部按网店建议零 售价销售完后,该零售商店获利不少于1980 元,那么小号小国旗的建议零售价至少 为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
(1)求线段DE的长度;
(2)如图2,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少;
(3)在(2)问的条件下,将得到的△CFP沿直线AE平移得到△C′F′P′,将△C′F′P′沿C′P′翻折得到△C′P′F″,记在平移过称中,直线F′P′与x轴交于点K,则是否存在这样的点K,使得△F′F″K为等腰三角形?若存在求出OK的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
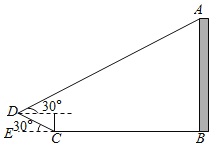
【题目】重庆由于丘陵、山地的特殊地势,被网友们称为”3D魔幻城市”.在重庆,你有时会看到马路上面是房屋、马路下面也是房屋;你从底楼出来,看到门口是一条公路,等你坐电梯上到顶楼,发现还是公路.小王家就在这样的一栋楼里:他从家里底楼出来会看到一条斜坡公路DC,已知∠DCE=30°,他从楼底B出发,沿着公路到达C处后继续沿着斜坡前进到达D处,共走了27![]() 米,然后他又沿着斜坡DA前进到达了顶楼A处,已知DA与水平线夹角为30°,大楼AB高
米,然后他又沿着斜坡DA前进到达了顶楼A处,已知DA与水平线夹角为30°,大楼AB高![]() 米,假设BC、CD、AD、AB在同一平面内,则斜坡CD的长度约为( )(已知:
米,假设BC、CD、AD、AB在同一平面内,则斜坡CD的长度约为( )(已知:![]() ≈1.73)
≈1.73)
A.10.3B.10.4C.9D.9.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com