
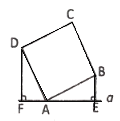
【题目】如图,直线![]() 过正方形
过正方形![]() 的顶点
的顶点![]() ,点
,点![]() 、
、![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 、
、![]() ,则正方形的周长为_________.
,则正方形的周长为_________.
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有三个分别标记为“1”、“2”、“3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记后放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记.
(1)请列出上述实验中所记录球上标记的所有可能的结果;
(2)求两次记录球上标记均为“1”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中 ,
中 ,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 的两边分别与
的两边分别与![]() ,
, ![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)如图,若![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
①写出![]() °,
°,![]() 的长是 .
的长是 .
②求四边形![]() 的周长.
的周长.

(2)如图,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,先补全图乙再证明
,先补全图乙再证明![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生小明将线段![]() 的垂直平分线
的垂直平分线![]() 上的点
上的点![]() ,称作线段
,称作线段![]() 的“轴点”.其中,当
的“轴点”.其中,当![]() 时,称
时,称![]() 为线段
为线段![]() 的“长轴点”;当
的“长轴点”;当![]() 时,称
时,称![]() 为线段
为线段![]() 的“短轴点”.
的“短轴点”.
(1)如图1,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,则在
,则在![]() ,
,![]() ,
,![]() ,
,![]() 中线段
中线段![]() 的“短轴点”是______.
的“短轴点”是______.

(2)如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() .
.

①若![]() 为线段
为线段![]() 的“长轴点”,则点
的“长轴点”,则点![]() 的横坐标
的横坐标![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
②点![]() 为
为![]() 轴上的动点,点
轴上的动点,点![]() ,
,![]() 在线段
在线段![]() 的垂直平分线
的垂直平分线![]() 的同侧.若
的同侧.若![]() 为线段
为线段![]() 的“轴点”,当线段
的“轴点”,当线段![]() 与
与![]() 的和最小时,求点
的和最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
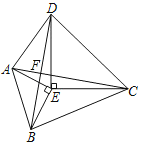
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com