Question

【题目】某市有三个景区是人们节假日游玩的热点景区，某学校对七（1）班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查，调查分四个类别，A：三个景区；B：游两个景区；C：游一个景区；D：不到这三个景区游玩，现根据调查结果绘制了如下不完全的条形统计图和扇形统计图，请结合图中信息解答下列问题：

（1）九（1）班现有学生__________人，在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________；

（2）请将条形统计图补充完整；

（3）若该校七年级有1000名学生，求计划“五一”小长假随父母到这三个景区游玩的学生多少名？

Answer 1

【答案】（1）50；72°；（2）补图见解析；（3）计划“五一”小长假随父母到这三个景区游玩的学生人数是600人．

【解析】试题分析：（1）根据图象得到信息.(2)先算出总人数，再分别计算度数,补充统计图.

(3)用总人数乘以去三个景区的百分比.

试题解析：

解：（1）∵A类5人，占10%，

∴八（1）班共有学生有：5÷10%=50（人）；

∴在扇形统计图中，表示“B类别”的扇形的圆心角的度数为： ×360°=72°；

故答案为：50，72°.

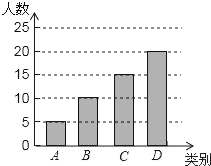
（2）D类：50﹣5﹣10﹣15=20（人），如图：

；

（3）计划“五一”小长假随父母到这三个景区游玩的学生人数是1000×（1﹣）=600（人）．

答：计划“五一”小长假随父母到这三个景区游玩的学生人数是600人．