
【题目】如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为___________

【答案】(2,3)
【解析】
过点C作CD⊥y轴于点D,通过角的计算可找出∠OAB=∠DBC,结合∠AOB=∠BDC、AB=BC,即可证出△OAB≌△DBC(AAS),根据全等三角形的性质即可得出BD=AO、DC=OB,再结合点A、B的坐标即可得出DC、OD的长度,进而可得出点C的坐标.
解:过点C作CD⊥y轴于点D,如图所示.
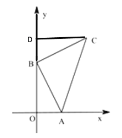
∵∠ABC=90°,∠AOB=90°,
∴∠OAB+∠OBA=90°,∠OBA+∠DBC=90°,
∴∠OAB=∠DBC.
在△OAB和△DBC中,
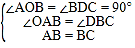 ,
,
∴△OAB≌△DBC(AAS),
∴BD=AO,DC=OB.
∵A(1,0)、B(0,2),
∴BD=AO=1,DC=OB=2,OD=OB+BD=3,
∴点C的坐标为(2,3).
故答案为:(2,3).


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
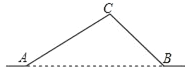
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
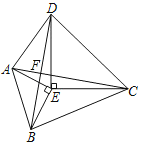
【题目】已知:等腰△DEC,∠DEC=90°,DE=EC=3,已知等腰△AEB,∠AEB=90°,AE=BE=2.
(l)求证:△DEB≌△CEA;
(2)判断BD与AC的关系,并说明理由.
(3)若∠DAE=90°,请直接写出BC的长,BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.
(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.
(2)请判断该游戏对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
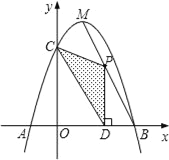
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆70周年前夕,网店销售 三种规格的手摇小国旗,其部分相关信息如下表:
型号 | 规格(mm) | 批发价(元/面) | 建议零售价(元/面) |
大号 | 45x30 | 2.00 | |
中号 | 28x20 | 1.50 | |
小号 | 22x14 |
已知大号小国旗比中号的批发价贵0.3元,小号小国旗比中号的批发价便宜0.1元某小商品零售商店,第一次用 380元购进了一批大号小国旗,紧接着又用780元购进了第二 批中号小国旗,第二批的数量是第一批的3倍.
(1)求三种型号小国旗的批发价分别是多少元?
(2)该商店很快又购进了第三批小号小国旗1200面.如果三批小国旗全部按网店建议零 售价销售完后,该零售商店获利不少于1980 元,那么小号小国旗的建议零售价至少 为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com