
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1,![]() ).
).
(1)求tan∠OPQ的值;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
【答案】(1)1;(2)①y=x2﹣2x+![]() ,;②A(
,;②A(![]() ,
,![]() )..
)..
【解析】
试题(1)求出于y轴交点,然后求tan∠OPQ的值.(2) ①先设出函数方程,再利用FQ′=OQ′,求出函数解析式.②把每一个点都用坐标表示出来,先求出FQ'解析式,利用FQ'⊥PK,求出PK解析式,求交点,再求出FK的解析式,与二次函数联立,得到A点坐标.
试题解析:
解:(1)∵y=x2﹣2x+1=(x﹣1)2,
∴顶点P(1,0),
∵当x=0时,y=1,
∴Q(0,1),
∴tan∠OPQ=1.
(2)①设抛物线C′的解析式为y=x2﹣2x+m,
∴Q′(0,m)其中m>1,
∴OQ′=m,
∵F(1,![]() ),
),
过F作FH⊥OQ′,如图:
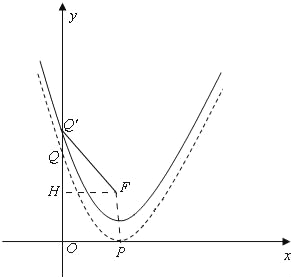
∴FH=1,Q′H=m﹣![]() ,
,
在Rt△FQ′H中,FQ′2=(m﹣![]() )2+1=m2﹣m+
)2+1=m2﹣m+![]() ,
,
∵FQ′=OQ′,
∴m2﹣m+![]() =m2,
=m2,
∴m=![]() ,
,
∴抛物线C′的解析式为y=x2﹣2x+![]() ,
,
②方法一:设点A(x0,y0),则y0=x02﹣2x0+![]() ①,
①,
过点A作x轴的垂线,与直线Q′F相交于点N,则可设N(x0,n),
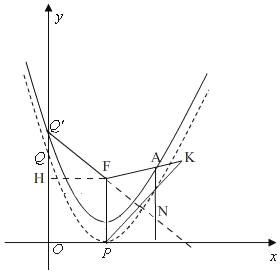
∴AN=y0﹣n,其中y0>n,
连接FP,
∵F(1,![]() ),P(1,0),
),P(1,0),
∴FP⊥x轴,
∴FP∥AN,
∴∠ANF=∠PFN,
连接PK,则直线Q′F是线段PK的垂直平分线,
∴FP=FK,有∠PFN=∠AFN,
∴∠ANF=∠AFN,则AF=AN,
∵A(x0,y0),F(1,![]() ),
),
∴AF2=(x0﹣1)2+(y0﹣![]() )2=x02﹣2x0+1+y02﹣y0+
)2=x02﹣2x0+1+y02﹣y0+![]() =x02﹣2x0+
=x02﹣2x0+![]() +y02﹣y0=(x02﹣2x0+
+y02﹣y0=(x02﹣2x0+![]() )+y02﹣y0,②
)+y02﹣y0,②
∵y0=x02﹣2x0+![]() ①,
①,
将①右边整体代换②得,AF2=(x02﹣2x0+![]() )+y02﹣y0=y0+y02﹣y0=y02,
)+y02﹣y0=y0+y02﹣y0=y02,
∵y0>0,
∴AF=y0,
∴y0=y0﹣n,
∴n=0,
∴N(x0,0),
设直线Q′F的解析式为y=kx+b,
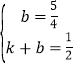 ,
,
解 ,
,
∴y=![]() x+
x+![]() ,
,
由点N在直线Q′F上,得,0=![]() x+
x+![]() ,
,
∴x0=![]() ,
,
将x0=![]() 代入y0=x2﹣2x0+
代入y0=x2﹣2x0+![]() ,
,
∴y0=![]() ,
,
∴A(![]() ,
,![]() ).
).
方法二:由①有,Q'(0,![]() ),F(1,
),F(1,![]() ),P(1,0),
),P(1,0),
∴直线FQ'的解析式为y=![]() x+
x+![]() ,①
,①
∵FQ'⊥PK,P(1,0),
∴直线PK的解析式为y=![]() x﹣
x﹣![]() ,②
,②
联立①②得出,直线FQ'与PK的交点M坐标为(![]() ,
,![]() ),
),
∵点P,K关于直线FQ'对称,
∴K(![]() ,
,![]() ),
),
∵F(1,![]() ),
),
∴直线FK的解析式为 y=![]() x+
x+![]() ③,
③,
∵射线FK与抛物线C′:y=x2﹣2x+![]() ④相交于点A,
④相交于点A,
∴联立③④得,,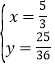 ,或
,或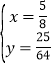 (舍),
(舍),
∴A(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中 ,
中 ,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 的两边分别与
的两边分别与![]() ,
, ![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)如图,若![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
①写出![]() °,
°,![]() 的长是 .
的长是 .
②求四边形![]() 的周长.
的周长.

(2)如图,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,先补全图乙再证明
,先补全图乙再证明![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
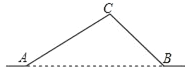
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)
查看答案和解析>>
科目:初中数学 来源: 题型:
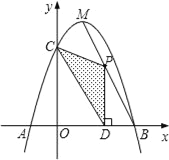
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com