
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
【答案】(1)a=1,b=3;(2)当m=![]() 时,PC有最大值,最大值为
时,PC有最大值,最大值为![]() .(3)若△PAC为直角三角形,点P的坐标为P1(2,6),P2(3,7).
.(3)若△PAC为直角三角形,点P的坐标为P1(2,6),P2(3,7).
【解析】
试题分析:(1)根据自变量与函数值的对应关系,可得b,根据待定系数法,可得a;
(2)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
(3)根据勾股定理,可得AP,CP的长,根据勾股定理的逆定理,可得关于m的方程,根据解方程,可得m的值,根据自变量与函数值的对应关系,可得答案.
解:(1)∵A(﹣1,b)在直线y=x+4上,
∴b=﹣1+4=3,
∴A(﹣1,3).
又∵A(﹣1,3)在抛物线y=ax(x﹣2)上,
∴3=﹣a(﹣1﹣2),
解得:a=1.
(2)设P(m,m+4),则C(m,m2﹣2m).
∴PC=(m+4)﹣(m2﹣2m)
=﹣m2+3m+4
=﹣(m﹣![]() )2+
)2+![]() ,
,
∵(m﹣![]() )2≥0,
)2≥0,
∴﹣(m﹣![]() )2+
)2+![]() ≤
≤![]() .
.
∴当m=![]() 时,PC有最大值,最大值为
时,PC有最大值,最大值为![]() .
.
(3)如图
 ,
,
P(m,m+4),C(m,m2﹣2m),
AP2=(m+1)2+(m+4﹣3)2=2(m+1)2,AC2=(m+1)2+(m2﹣2m﹣3)2,PC2=(﹣m2+3m+4)2.
①当AP2+AC2=PC2时,即2(m+1)2+(m+1)2+(m2﹣2m﹣3)2=(﹣m2+3m+4)2,
3(m+1)2+[(m2﹣2m﹣3)2﹣(﹣m2+3m+4)2]=0
化简,得(m+1)(m+1)(m﹣2)=0,
解得m=﹣1(不符合题意,舍),m=2,
当m=2时,m+4=6,即P(2,6);
②当AP2=AC2+PC2时,即2(m+1)2=(m+1)2+(m2﹣2m﹣3)2+(﹣m2+3m+4)2,
化简,得
(m﹣4)(m+1)(m+1)(m﹣3)=0.
解得m=4(不符合题意,舍),m=﹣1(不符合题意,舍),m=3,
当m=3时,m+4=7,
即(3,7),
综上所述:若△PAC为直角三角形,点P的坐标为P1(2,6),P2(3,7).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )

A.1处 B.2处 C.3处 D.4处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月19日,重庆市第五届运动会开幕式将在溶陵区拉开大幕,组委会面向社会公开征集了主题门号、会徽、会歌,吉祥物等元素,共收到有效作品1600余件,数据1600用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx﹣1与y=x﹣1平行,则y=kx﹣1的图象经过的象限是( )
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将二次函数y=3x2的图象向上平移5个单位,得到新的图象的二次函数表达式是( )
A.y=3x2-5 B.y=3(x-5)2
C.y=3x2+5 D.y=3(x+5)2-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
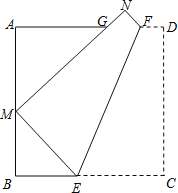
(1)△AGM∽△BME;
(2)若M为AB中点,则![]() =
=![]() =
=![]() ;
;
(3)△AGM的周长为2a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
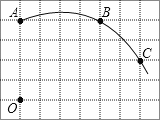
(1)请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C 、D ;
②⊙D的半径= (结果保留根号);
③∠ADC的度数为 .
④网格图中是否存在过点B的直线BE是⊙D的切线?如果没有,请说明理由;如果有,请直接写出直线BE的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com