
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
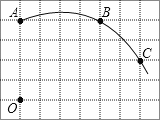
(1)请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C 、D ;
②⊙D的半径= (结果保留根号);
③∠ADC的度数为 .
④网格图中是否存在过点B的直线BE是⊙D的切线?如果没有,请说明理由;如果有,请直接写出直线BE的函数解析式.
【答案】(1)见解析;(2)①(6、2)(2、0);②2![]() ;③90°;④y=﹣
;③90°;④y=﹣![]() x+6
x+6
【解析】
试题分析:(1)根据图形和垂径定理画出图形即可;
(2)①根据已知和网格得出即可;
②根据勾股定理求出半径即可;
③证△AOD≌△DFC,根据全等得出∠OAD=∠CDF,即可求出答案;
④先画出图形,求出B、M的坐标,设出直线BE的解析式,代入求出即可.
解:(1)如图1所示:
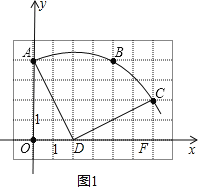 ;
;
(2)C(6,2),D(2,0),
①故答案为:(6、2)(2、0);
②⊙D的半径为:![]() =2
=2![]() ,
,
故答案为:2![]() ;
;
③∵OA=DF=4,CF=OD=2,∠AOD=∠DFC=90°,
∴在△AOD和△DFC中
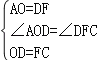
∴△AOD≌△DFC(SAS),
∴∠OAD=∠CDF,
∵∠AOD=90°,
∴∠ADC=180°﹣(∠ADO+∠CDF)
=180°﹣(∠ADO+∠OAD)
=∠AOD
=90°,
故答案为:90°;
④如图2,存在过点B的直线BE是⊙D的切线,
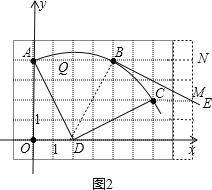
则∠DBE=90°,
与③类似可得出△DQB≌△BNM,
所以QD=BN=4,MN=QB=2,
则点M的坐标为(8,2),B的坐标为(4,4),
设直线BE的解析式为y=kx+b(k、b为常数,k≠0),
把B、M的坐标代入得:![]() ,
,
解得:k=﹣![]() ,b=6.
,b=6.
故BE的解析式为y=﹣![]() x+6.
x+6.


科目:初中数学 来源: 题型:
【题目】下列实际情景运用了三角形稳定性的是( )
A. 人能直立在地面上 B. 校门口的自动伸缩栅栏门
C. 古建筑中的三角形屋架 D. 三轮车能在地面上运动而不会倒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有三个分别标记为“1”、“2”、“3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记后放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记.
(1)请列出上述实验中所记录球上标记的所有可能的结果;
(2)求两次记录球上标记均为“1”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳妈妈要给一幅长为60cm,宽为40cm的矩形十字绣的四周装裱一条宽度相同的金色边框制成一幅矩形挂图,使整幅挂图面积是3400cm2.设金色边框的宽度为x cm,则x满足的方程是( )
A.x2+50x﹣1400=0
B.x2﹣65x﹣250=0
C.x2﹣30x﹣1400=0
D.x2+50x﹣250=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
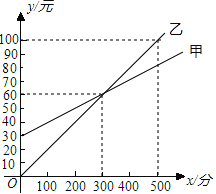
(1)有月租费的收费方式是 (填甲或乙),月租费是 元;
(2)求出甲、乙两种收费方式中y与自变量x之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com