Question

【题目】如图，折叠边长为a的正方形ABCD，使点C落在边AB上的点M处（不与点A，B重合），点D落在点N处，折痕EF分别与边BC、AD交于点E、F，MN与边AD交于点G．证明：

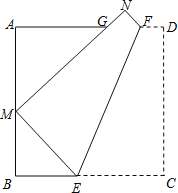
（1）△AGM∽△BME；

（2）若M为AB中点，则==；

（3）△AGM的周长为2a．

Answer 1

【答案】见解析

【解析】

试题分析：（1）根据正方形的性质和折叠的性质得出∠A=∠B，∠AGM=∠BME，再利用相似三角形的判定证明即可；

（2）设BE=x，利用勾股定理得出x的值，再利用相似三角形的性质证明即可；

（3）设BM=x，AM=a﹣x，利用勾股定理和相似三角形的性质证明即可．

证明：（1）∵四边形ABCD是正方形，

∴∠A=∠B=∠C=90°，

∴∠AMG+∠AGM=90°，

∵EF为折痕，

∴∠GME=∠C=90°，

∴∠AMG+∠BME=90°，

∴∠AGM=∠BME，

在△AGM与△BME中，

∵∠A=∠B，∠AGM=∠BME，

∴△AGM∽△BME；

（2）∵M为AB中点，

∴BM=AM=，

设BE=x，则ME=CE=a﹣x，

在Rt△BME中，∠B=90°，

∴BM2+BE2=ME2，即（）2+x2=（a﹣x）2，

∴x=a，

∴BE=a，ME=a，

由（1）知，△AGM∽△BME，

∴===，

∴AG=BM=a，GM=ME=a，

∴==；

（3）设BM=x，则AM=a﹣x，ME=CE=a﹣BE，

在Rt△BME中，∠B=90°，

∴BM2+BE2=ME2，即x2+BE2=（a﹣BE）2，

解得：BE=﹣，

由（1）知，△AGM∽△BME，

∴==，

∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x，

∴C△AGM=C△BME=（a+x）=2a．