【题目】已知关于
的方程
有两个实数根
，
．
求
的取值范围；
若
，求的值．
【答案】（1）
的取值范围是
；; （2）的值是
．
【解析】
（1）方程有两个实数根，可得△=b2﹣4ac≥0，代入可解出k的取值范围；
（2）结合（1）中k的取值范围，由题意可知，x1+x2=2（k﹣1）＜0，去绝对值符号结合等式关系，可得出k的值．
（1）由方程有两个实数根，可得
△=b2﹣4ac=4（k﹣1）2﹣4k2=4k2﹣8k+4﹣4k2=﹣8k+4≥0，解得：k≤
；
（2）依据题意可得：x1+x2=2（k﹣1），x1x2=k2，由（1）可知k≤，∴2（k﹣1）＜0，x1+x2＜0，∴﹣x1﹣x2=﹣（x1+x2）=x1x2﹣1，∴﹣2（k﹣1）=k2﹣1，解得：k1=1（舍去），k2=﹣3，∴k的值是﹣3．
答：（1）k的取值范围是k≤；（2）k的值是﹣3．
科目：初中数学 来源： 题型：
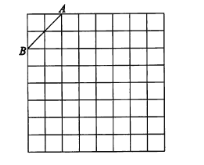
【题目】如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：
(1)在网格中建立平面直角坐标系，使A点坐标为(-2，4)，B点坐标为(-4，2)；
(2)在(1)的前提下，在第二象限内的格点上找一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点的坐标是；
(3)求((2)中△ABC的周长(结果保留根号)；
(4)画出((2)中△ABC关于y轴对称的△A'B'C'.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两名学生参加数学素质测试（有四项），每项测试成绩采用百分制，成绩如表：
学生 | 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | 平均成绩 | 方差 |
甲 | 87 | 93 | 91 | 85 | 89 | ______ |
乙 | 89 | 96 | 91 | 80 | ______ | ______ |
（1）将表格中空缺的数据补充完整，根据表中信息判断哪个学生数学综合素质测试成绩更稳定？请说明理由.
（2）若数与代数、空间与图形、统计与概率、综合与实践的成绩按
，计算哪个学生数学综合素质测试成绩更好？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
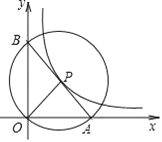
【题目】如图，在平面直角坐标系中，O 为坐标原点，P是反比例函数
图象上任意一点，以P为圆心，PO为半径的圆与x轴交于点 A、与y轴交于点B，连接AB．
（1）求证：P为线段AB的中点；
（2）求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△
C；平移△ABC，若A的对应点
的坐标为（0，4），画出平移后对应的△
；
（2）若将△C绕某一点旋转可以得到△，请直接写出旋转中心的坐标；
（3）在
轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料:
分解因式：
请根据上述材料回答下列问题：
（1）小云的解题过程从 步出现错误的，错误的原因是： .
小朵的解题过程从 步出现错误的，错误的原因是 .
小天的解题过程从 步出现错误的，错误的原因是： .
（2）若都不正确，请你写出正确的解题过程.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学生小明将线段
的垂直平分线
上的点
，称作线段的“轴点”.其中，当
时，称为线段的“长轴点”；当
时，称为线段的“短轴点”.
（1）如图1，点
，
的坐标分别为
，
，则在
，
，
，
中线段的“短轴点”是______.
（2）如图2，点的坐标为
，点在
轴正半轴上，且
.
①若为线段的“长轴点”，则点的横坐标
的取值范围是（ ）
A.
B.
C.
D.或
②点
为轴上的动点，点，在线段的垂直平分线的同侧.若
为线段的“轴点”，当线段
与
的和最小时，求点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为评估九年级学生的学习成绩状况，以应对即将到来的中考做好教学调整，某中学抽取了部分参加考试的学生的成绩，绘制成了如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：
（1）本次调查共抽取了多少名学生？
（2）通过计算补全条形统计图；
（3）该校九年级共有1000人参加了这次考试，请估算该校九年级共有多少名学生的学习成绩达到优秀.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
