
【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图: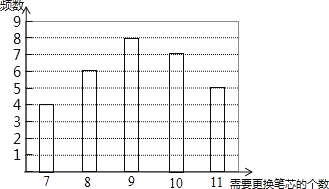
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若n=9,求y与x的函数关系式;
(2)若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.
【答案】
(1)
解:当n=9时,y= ![]() =
= ![]()
(2)
解:根据题意,“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,则“更换笔芯的个数不大于同时购买笔芯的个数”的频数大于30×0.5=15,
根据统计图可得,需要更换笔芯的个数为7个对应的频数为4,8个对应的频数为6,9个对应的频数为8,
因此当n=9时,“更换笔芯的个数不大于同时购买笔芯的个数”的频数=4+6+8=18>15.
因此n的最小值为9.
(3)
解:若每支笔同时购买9个笔芯,
则所需费用总和=(4+6+8)×3×9+7×(3×9+5×1)+5×(3×9+5×2)=895,
若每支笔同时购买10个笔芯,
则所需费用总和=(4+6+8+7)×3×10+5×(3×10+5×1)=925,
因此应购买9个笔芯.
【解析】(1)根据题意列出函数关系式;
(2)由条形统计图得到需要更换笔芯的个数为7个对应的频数为4,8个对应的频数为6,9个对应的频数为8,即可.
(3)分两种情况计算 此题是一次函数的应用,主要考查了一次函数的性质,统计图,解本题的关键是统计图的分析.
【考点精析】认真审题,首先需要了解频数与频率(落在各个小组内的数据的个数为频数;每一小组的频数与数据总数(样本容量n)的比值叫做这一小组的频率),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的6![]() 6网格中,A,B,C是格点(我们把组成网格的小正方形的顶点,称为格点),其中点C在直线AB外。
6网格中,A,B,C是格点(我们把组成网格的小正方形的顶点,称为格点),其中点C在直线AB外。
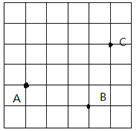
(1)过A点画AB的垂线AG;
(2)过C点画AB的平行线CH;
(3)连接BC,线段BC与线段AB的关系:______________;
(4)_____________________是点C到直线AB的距离;
(5)因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段AC,BC的大小关系是______________(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2 ![]() ,反比例函数y=
,反比例函数y= ![]() (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D. 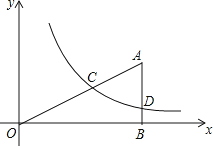
(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.


![]() 图2的阴影部分的正方形的边长是______.
图2的阴影部分的正方形的边长是______.
![]() 用两种不同的方法求图中阴影部分的面积.
用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = ____________;
= ____________;
(方法2)![]() = ____________;
= ____________;
(3) 观察图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
![]() 根据
根据![]() 题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,在平面直角坐标系中,若已知点A(xA,yA)和点C(xC,yC),点M为线段AC的中点,利用三角形全等的知识,有△AMP≌△CMQ,则有PM=MQ,PA=QC,即xM﹣xA=xC﹣xM,yA﹣yM=yM﹣yC,从而有 ,即中点M的坐标为(
,即中点M的坐标为(![]() ,
,![]() ).
).

基本知识:
(1)如图①,若A、C点的坐标分别A(﹣1,3)、C(3,﹣1),求AC中点M的坐标;
方法提炼:
(2)如图②,在平面直角坐标系中,ABCD的顶点A、B、C的坐标分别为(﹣1,5)、(﹣2,2)、(3,3),求点D的坐标;
(3)如图③,点A是反比例函数y=![]() (x>0)上的动点,过点A作AB∥x轴,AC∥y轴,分别交函数y═
(x>0)上的动点,过点A作AB∥x轴,AC∥y轴,分别交函数y═![]() (x>0)的图象于点B、C,点D是直线y=2x上的动点,请探索在点A运动过程中,以A、B、C、D为顶点的四边形能否为平行四边形,若能,求出此时点A的坐标;若不能,请说明理由.
(x>0)的图象于点B、C,点D是直线y=2x上的动点,请探索在点A运动过程中,以A、B、C、D为顶点的四边形能否为平行四边形,若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐标;
②画出“基本图形”绕B点顺时针旋转90°所成的四边形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com