
【题目】如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1).
①画出“基本图形”关于原点O对称的四边形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐标;
②画出“基本图形”绕B点顺时针旋转90°所成的四边形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
科目:初中数学 来源: 题型:
【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图: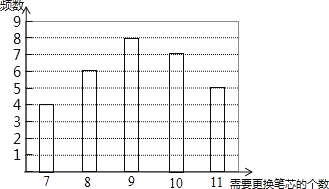
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若n=9,求y与x的函数关系式;
(2)若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线 ![]() 上,则旋转中心P的坐标为。
上,则旋转中心P的坐标为。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( ) 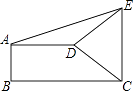
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2= ![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 ![]() = .
= . 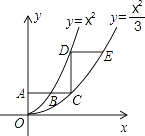
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC外作△ABD和△ACE,使AD=AB,AE=AC,且∠DAB=∠EAC,连接BE,CD相交于P点,求证:点A在∠DPE的平分线上.
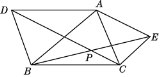
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用 水量x/m3 | 0< x≤5 | 5< x≤10 | 10< x≤15 | 15< x≤20 | x>20 |
频数/户数 | 12 | 20 | 3 | ||
百分比 | 12% | 7% |
若该小区有800户家庭,据此估计该小区月均用水量不超过10 m3的家庭有________户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M,N分别以每秒1个单位的速度从点A,D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M,N同时停止运动.设运动时间为t秒.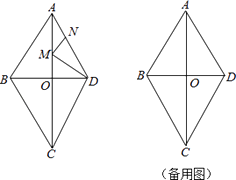
(1)求菱形ABCD的周长.
(2)设△DMN的面积为S,求S关于t的解析式,并求S的最大值(提示:需分两种情况讨论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com