
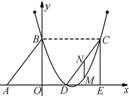
如图,Rt△ABO的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A,B两点的坐标分别为(-3,0),(0,4),抛物线y=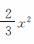 +bx+c经过点B,且顶点在直线
+bx+c经过点B,且顶点在直线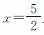 上.
上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若点M是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
科目:初中数学 来源: 题型:
某家电集团公司研制生产的新家电,前期投资200万元,每生产一台这种新家电,后期还需投资0.3万元。已知每台新家电售价为0.5万元。设总投资为P万元,总利润为Q万元(总利润=总产值-总投资),新家电总产量为x台。(假设可按售价全部卖出)
(1)试用x的代数式表示P和Q;
(2)当总产量达到900台时,该公司能否盈利?
(3)当总产量达到多少台时,该公司开始盈利?
查看答案和解析>>
科目:初中数学 来源: 题型:
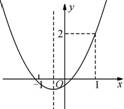
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③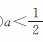 ④b>1.其中正确的结论是( ).
④b>1.其中正确的结论是( ).
A. ①② B. ②③
C. ③④ D. ②④
(第4题)
查看答案和解析>>
科目:初中数学 来源: 题型:
为了进一步落实“节能减排”措施,冬季供暖来临前,某单位决定对9000平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务.问甲队每天完成多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com