
分析 (1)根据一个窗口平均每小时的售票量乘以窗口的个数、乘以售票的时间,可得答案;
(2)根据一个窗口平均每小时的售票量乘以窗口的个数乘以售票的时间,可得答案;
(3)根据售票总量除以除以一个窗口4小时的售票量,可得售票窗口数;
(4)根据售票总量除以8个窗口一小时的售票量,可得售票时间.
解答 解:(1)由题意,得
30×4×5=600
答:当天一共售出600张票;
(2)设开发x个售票窗口时,需要y个小时才能使当天购票的旅客全部买到票,试求y与x之间的函数关系式.
30xy=600
y=$\frac{20}{x}$,
y与x之间的函数关系式为y=$\frac{20}{x}$;
(3)如果准备在4个小时内是当天购票的旅客全部买到票,那么至少要开放窗口$\frac{600}{4×30}$=5(个)
答:至少要开发5个售票窗口;
(4)客运站售票大厅最多可以同时开放8个售票窗口,那么最少时间$\frac{600}{30×8}$=$\frac{5}{2}$(小时),
答:最少$\frac{5}{2}$时可以使当天购票的旅客全部买到票.
点评 本题考查了反比例函数的应用,利用了一个窗口平均每小时的售票量乘以窗口的个数、乘以售票的时间等于总售票量.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}+1}{{x}^{2}}$ | B. | $\frac{x-1}{{x}^{2}-1}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x-1}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
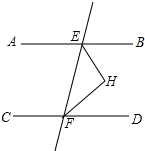 如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
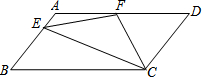 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
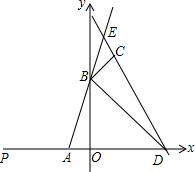 如图,在平面直角坐标系中,直线y=3x+3分别交x轴,y轴于点A、B,直线y=-2x+6过点C(1,4)且交x轴于点D,直线AB与直线CD交于点E.
如图,在平面直角坐标系中,直线y=3x+3分别交x轴,y轴于点A、B,直线y=-2x+6过点C(1,4)且交x轴于点D,直线AB与直线CD交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com