
(本题10分)已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F, 交AD于N,交AB于M,连接ME。

(1)求证:ME⊥BC;
(2)若AB= ,试求ME的长。
,试求ME的长。
(2)1
【解析】
试题分析:(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,再求出∠ACF=45°,从而得到∠B=∠ACF,根据同角的余角相等求出∠BAE=∠CAF,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等证明即可;
(2)根据等腰三角形的性质可以得到要相等,在根据勾股定理得到斜边的长,然后根据等腰三角形的性质得出CE的长,从而求出BE,最终根据等腰三角形的性质求出结果.
试题解析:(1)∵AE平分∠BAD
∴∠BAE=∠EAD
又∵∠BAC=90°,AD⊥BC
∴∠EAC=90°-∠BAE; ∠AED=90°-∠EAD
∴∠EAC=∠AED
∴AC=EC
∵CM⊥AE
∴∠ACM=∠ECM 又CM=CM
∴△ACM≌△ECM(SAS)
∴∠MEC=∠MAC=90°
即 ME⊥BC
(2)在Rt△ABC中,AB=AC=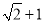
∴BC=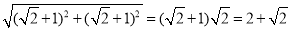
又CE=AC=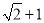
∴BE=BC-CE=(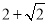 )-(
)-(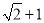 )=1
)=1
∵ME⊥BC, ∠B=45°
∴∠BME=∠B
∴ME=BE=1
考点:等腰三角形的性质与判定,勾股定理,三角形全等的判定与性质


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:填空题
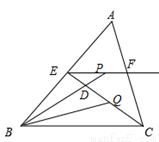
如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=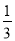 CE时,EP+BP= .
CE时,EP+BP= .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第四次月考数学试卷(解析版) 题型:选择题
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是: ( )
①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.

A. ①②④ B.①③④ C. ①② D.②③
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市崇安区七年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,数轴上每相邻两点之间相距1个单位长度,点A对应的数为a,B对应的数为b,且b-
2a=7,那么数轴上原点的位置在( )
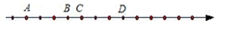
A.点A B .点B C.点C D.点D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com