
【题目】某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,AB=![]() CD=
CD=![]() m,BC=3
m,BC=3![]() m,试求这块空地的面积.
m,试求这块空地的面积.
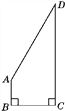
【答案】![]() (m2)
(m2)
【解析】试题分析:过点A作AE⊥DC于点E,根据AB=![]() CD=
CD=![]() m即可求出DE、CD的值,进而利用勾股定理求出AD的值;根据矩形以及直角三角形的面积公式以及周长的计算方法,即可解决.
m即可求出DE、CD的值,进而利用勾股定理求出AD的值;根据矩形以及直角三角形的面积公式以及周长的计算方法,即可解决.
试题解析:过点A作AE⊥DC于点E,如图所示.
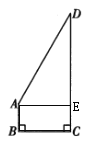
∵AB=![]() CD=
CD=![]() m,AE⊥CD,
m,AE⊥CD,
∴CD=4![]() m ,DE=3
m ,DE=3![]() m,
m,
∵AB⊥BC,CD⊥BC ,AE⊥CD, BC=3![]() m,
m,
∴四边形ABCE为矩形,
∴AE=BC=3![]() m,
m,
∵AE=3![]() m ,DE=3
m ,DE=3![]() m,
m,
∴AD=6![]() m,
m,
∵四边形ABCE为矩形,△AED为直角三角形,
∴空地的周长=AB+BC+CD+AD=9![]() +5
+5![]() (m)
(m)
空地的面积=AB·BC+![]() AE·DE=15
AE·DE=15![]() (m3).
(m3).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】某花卉基地出售两种盆栽花卉:太阳花的价格为6元/盆,绣球花的价格为10元/盆.若一次性购买绣球花超过20盆时,超过20盆的部分绣球花打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数表达式.
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花的数量不超过绣球花数量的一半,则两种花卉各买多少盆时,总费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,并回答有关问题:![]() ;
;![]() ;
;![]() ;
;
…
(1)若n为正整数,猜想13+23+33+…+n3的值;
(2)利用上题的结论比较13+23+33+…+1003与50002的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com