
����Ŀ��ij���ܻ��س����������Ի��ܣ�̫�����ļ۸�Ϊ6Ԫ/�������ļ۸�Ϊ10Ԫ/������һ���Թ���������20��ʱ������20��IJ�������8����
(1)�ֱ�д�����ֻ��ܵĸ�����y(Ԫ)���ڹ�����x(��)�ĺ�������ʽ��
(2)Ϊ��������������С���ƻ����û��ع��������ֻ��ܹ�90��������̫��������������������������һ���������ֻ��ܸ��������ʱ���ܷ������٣������ܷ���Ϊ����Ԫ��
���𰸡���1��y=6x��y=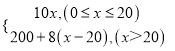 ��2����x��60������������60��������̫����30��ʱ���ܷ��������������ܷ���Ϊ700Ԫ
��2����x��60������������60��������̫����30��ʱ���ܷ��������������ܷ���Ϊ700Ԫ
�����������������(1)��̫�����ļ۸�=6�����������ļ۸��x��20��x��20��������ֱ���м��㣬�ó���������ʽ��(2)��������̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ�������������m��ȡֵ��Χ��Ȼ��ó�w��m�ĺ�����ϵʽ��Ȼ�����һ�κ����������Եó���Сֵ.
���������(1)��y̫����=6x��
��y����=10x��x��20����
��y����=10��20+10��0.8����x-20��=200+8x-160=8x+40��x��20��
(2)���������⣬ ��̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ��
��m��![]() (90-m) ��m��30��
(90-m) ��m��30��
��w=6m+[8��90-m��+40]=760-2m
��-2��0 ��w����m���������С�� ����m=30ʱ��
w��С=760-2��30=700��Ԫ����
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾2�·ݵ�����Ϊ160��Ԫ��4�·ݵ�����250��Ԫ������ƽ��ÿ�µ�������x�����������ɵ÷���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���kx2-2x-1=0����������ȵ�ʵ��������ʵ��k��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M����4����1������y��ԳƵĵ������Ϊ�� ��
A.����4��1��
B.��4��1��
C.��4����1��
D.����4����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
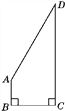
����Ŀ��ijУһ��յر��ķϣ���ͼ��Ϊ���̻�������ѧУ�����������յ���ֲ���ݣ���֪AB��BC��CD��BC��AB��![]() CD��
CD��![]() m��BC��3
m��BC��3![]() m���������յص������
m���������յص������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ȱ�װ���˷���Դ����Ⱦ�������ݲ��㣬���ȫ��ÿ�����10%�Ĺ��Ȱ�װֽ��������ô�ɼ��Ŷ�����̼3120000�֣�����3120000�ÿ�ѧ��������ʾΪ��������
A. 3.12��106 B. 3.12��105 C. 31.2��105 D. 0.312��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��MA1��NA2 �� ���A1+��A2= �ȣ�
��ͼ2��MA1��NA3 �� ���A1+��A2+��A3= �ȣ�
��ͼ3��MA1��NA4 �� ���A1+��A2+��A3+��A4= �ȣ�
��ͼ4��MA1��NA5 �� ���A1+��A2+��A3+��A4+��A5= �ȣ��������������㷢����ʲô���ɣ�
��ͼ5��MA1��NAn �� ���A1+��A2+��A3+��+��An= �ȣ�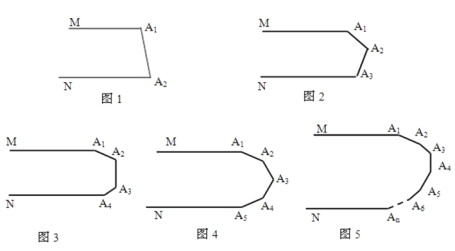
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=x2+��2m��1��x+m2��1��������ԭ�㣬�ҵ�x��0ʱ��y��x���������С��
��1���������ߵĽ���ʽ����д��y��0ʱ����Ӧx��ȡֵ��Χ��
��2�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB��x���ڵ�B��DC��x���ڵ�C��
����BC=1ʱ��ֱ��д������ABCD���ܳ���
���趯��A������Ϊ��a��b����������ABCD���ܳ�L��ʾΪa�ĺ�����д���Ա�����ȡֵ��Χ���ж��ܳ��Ƿ�������ֵ��������ڣ����������ֵ���������ʱ��A�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com