
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
【答案】(1)y<0时,0<x<3;(2)①矩形的周长为6;②当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式,根据函数的增减性,可得符合条件的函数解析式,根据函数与不等式的关系,可得答案;
(2)①根据BC关于对称轴对称,可得A点的纵坐标,根据矩形的周长公式,可得答案;
②分类讨论A在对称轴左侧,A在对称轴右侧,根据对称,可得BC的长,AB的长,根据周长公式,可得函数解析式,根据函数的增减性,可得答案.
试题解析:(1)∵抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点(0,0),∴m2﹣1=0,∴m=±1,
∴y=x2+x或y=x2﹣3x,∵当x<0时,y随x的增大而减小,∴y=x2﹣3x,由函数与不等式的关系,得y<0时,0<x<3;
(2)①如图1
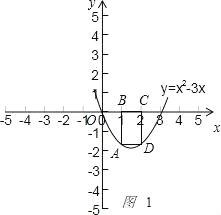 ,
,
当BC=1时,由抛物线的对称性,得点A的纵坐标为﹣2,
∴矩形的周长为6;
②∵A的坐标为(a,b),
∴当点A在对称轴左侧时,如图2
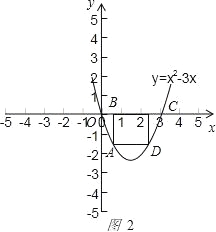 ,
,
矩形ABCD的一边BC=3﹣2a,另一边AB=3a﹣a2,
周长L=﹣2a2+2a+6.其中0<a<![]() ,当a=
,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当点A在对称轴右侧时如图3
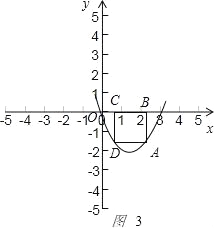 ,
,
矩形的一边BC=3﹣(6﹣2a)=2a﹣3,另一边AB=3a﹣a2,
周长L=﹣2a2+10a﹣6,其中![]() <a<3,当a=
<a<3,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() );
);
综上所述:当0<a<![]() 时,L=﹣2(a﹣
时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当![]() <a<3时,L=﹣2(a﹣
<a<3时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
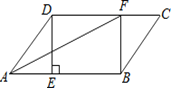
【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AD=DF,求证:AF平分∠BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是必然事件是( )
A.明天太阳从西边升起
B.篮球队员在罚球线投篮一次,未投中
C.实心铁球投入水中会沉入水底
D.抛出一枚硬币,落地后正面向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
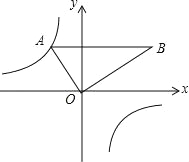
【题目】如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
(1)求双曲线的解析式;
(2)把三角板AOB绕点A顺时针旋转,使得点O的对应点C落在x轴的负半轴上的对应线段为AD,试判断点D是否在双曲线上?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com