Question

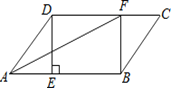
【题目】如图，在□ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF.

（1）求证：四边形BFDE是矩形；

（2）若AD=DF，求证:AF平分∠BAD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．

试题解析：

（1）证明：∵四边形ABCD是平行四边形，

∴AB∥CD．

∵BE∥DF，BE=DF，

∴四边形BFDE是平行四边形．

∵DE⊥AB，

∴∠DEB=90°，

∴四边形BFDE是矩形；

（2）解：∵四边形ABCD是平行四边形，

∴AB∥DC，

∴∠DFA=∠FAB．

在Rt△BCF中，由勾股定理，得
BC=

∴AD=BC=DF=5，
∴∠DAF=∠DFA，
∴∠DAF=∠FAB，
即AF平分∠DAB．