
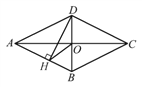
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列事件中,是必然事件的为( )
A.3天内会下雨
B.打开电视,正在播放广告
C.367人中至少有2人公历生日相同
D.某妇产医院里,下一个出生的婴儿是女孩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b都有:a⊕b=a(a+b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2+5)+1=2×7+1=15,那么不等式-3⊕x<13的解集为 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
A. q<16 B. q>16 C. q≤4 D. q≥4
查看答案和解析>>
科目:初中数学 来源: 题型:
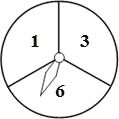
【题目】如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若多项式x2+ax+b分解因式的结果(x﹣2)(x+3),则a,b的值分别是( )
A.a=1,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=5,b=﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.DF=8.
(1)若P是BC上的一个动点,当PA=DF时,求此时∠PAB的度数;
(2)将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
①求证:AD∥BF;
②若P是BC的中点,连接FP,将等腰直角三角板ABC绕点B继续旋转,当旋转角α= 时,FP长度最大,最大值为 (直接写出答案即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com