
����Ŀ����һ��ֱ�����ǰ���ͼ�ٰڷţ��ܹ����ֵ���ֱ�����ǰ�ABC��б���뺬30��ǵ�ֱ�����ǰ�DEF�ij�ֱ�DZ�DE�غϣ�DF=8��
��1����P��BC�ϵ�һ�����㣬��PA=DFʱ�����ʱ��PAB�Ķ�����
��2����ͼ���еĵ���ֱ�����ǰ�ABC�Ƶ�B˳ʱ����ת30�㣬��C����BF�ϣ�AC��BD���ڵ�O������CD����ͼ�ڣ�
����֤��AD��BF��
����P��BC���е㣬����FP��������ֱ�����ǰ�ABC�Ƶ�B������ת������ת�Ǧ�= ʱ��FP����������ֵΪ ��ֱ��д���𰸼��ɣ���

���𰸡���1����PAB�Ķ���Ϊ15���75�㣻
��2���������������
��210�㣬16+4![]() ��
��
��������
�����������1������������Ǻ��������APH��Ȼ�������������㼴�ɣ�
��2��������AM��BC��DN��BC���õ�AM��DN���ڼ����AM��DN���õ�AM=DN������ƽ���ı���AMND�������жϳ�PF���ʱ����P����FB���ӳ����ϣ�����⼴�ɣ�
��ͼ1��
 D��
D��
�����������1����AH��BC��H����AH=![]() BC����DF=8����DEF=30�㣬��BC=DE=
BC����DF=8����DEF=30�㣬��BC=DE=![]() =8
=8![]() ��
��
��AH=4![]() ����PA=DF=8ʱ��sin��APH=
����PA=DF=8ʱ��sin��APH=![]() =
=![]() �����APH=60�㣬
�����APH=60�㣬
���ߡ�ABC=45�㣬��AP1H=60�㣬���BAP1=��AP1H����ABC=15�㣬
���ߡ�ACB=45�㣬��AP2H=60�㣬���CAP2=��AP2B����ACB=15�㣬
�ߡ�BAC=90�㣬���BAP2=90�㩁��CAP2=75�㣻���PAB�Ķ���Ϊ15���75�㣻
��2������ͼ2��AM��BC��DN��BC����Rt��ABC�У�AB=AC��BC=8![]() ��
��
��AM=![]() BC=
BC=![]() ��8
��8![]() =4
=4![]() ����Rt��BCF�У���F=60�㣬DF=8����DN=DF��sin��F=8��
����Rt��BCF�У���F=60�㣬DF=8����DN=DF��sin��F=8��![]() =4
=4![]() ��
��
��AM=DN����AM��DN�����ı���AMND��ƽ���ı��Σ���AD��BC��

����P��BC���е㣬��FP����������е�F��B��P��ͬһ��ֱ���ϣ�
������P��FB���ӳ����ϣ�
��BC����ת180�㣬
�ߡ�CDF=30�㣬
����ת�Ǧ�=210�㣬
��P��BC���е㣬BC=8![]() ��
��
��BP=4![]() ��
��
��BF=2DF=16��
��FP=16+4![]() ��
��
�ʴ�Ϊ210�㣬16+4![]() ��
��


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCD������,�Խ���AC,BD�ཻ�ڵ�O,DH��AB��H,����OH,��֤:��DHO=��DCO.
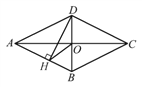
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ѻ�30���ǵ����ǰ��������ͼ��ʾ��ƽ��ֱ������ϵ�У���AOB=90������B=30����OA=2��б��AB��x�ᣬ��A��˫�����ϣ�
��1����˫���ߵĽ���ʽ��
��2�������ǰ�AOB�Ƶ�A˳ʱ����ת��ʹ�õ�O�Ķ�Ӧ��C����x��ĸ������ϵĶ�Ӧ�߶�ΪAD�����жϵ�D�Ƿ���˫�����ϣ���˵�����ɣ�
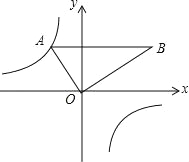
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȩ�1С2017�����ǣ�������
A. ��2016 B. 2016 C. 2018 D. ��2018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC=4��D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���ED��FD������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�
��AE=CF��
��EF���ֵΪ2![]() ��
��
���ı���CEDF����������Eλ�õĸı�������仯��
�ܵ�C���߶�EF��������Ϊ![]() ��
��
���н�����ȷ���� ����������ȷ�𰸵���Ŷ���д�ں����ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA����2��1����B����4��5����C����5��2����
��1��������ABC����x��ԳƵ���A1B1C1��
��2��������ABC����ԭ��O�����ĶԳƵ���A2B2C2��
��3��������ABC��Բ��O˳ʱ����ת90�����A3B3C3��
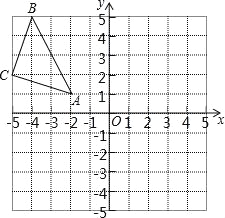
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ����ƷA����۵�9�۳���(���Ż�10%)�Կɻ�����10%������ƷA�ı��Ϊ33Ԫ�������Ʒ�Ľ���Ϊ( )
A. 27Ԫ B. 29.7Ԫ C. 30.2Ԫ D. 31Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij������ʻ��·��s(km)��ʱ��t(����) �ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ������������⣺
��1����������ǰ9�����ڵ�ƽ���ٶ�.
��2����������;ͣ����ʱ��.
��3�����������ʻ30ǧ��ʱ��.
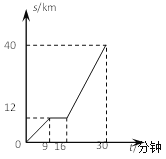
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��2(x��3)2��2��ͼ������������ȷ����( )
A. ��������Ϊ(��3��2) B. �Գ���Ϊֱ��x����3
C. ��x��3ʱ��y��x����������� D. ��x��3ʱ��y��x���������С
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com