
【题目】观察下列等式,并回答有关问题:![]() ;
;![]() ;
;![]() ;
;
…
(1)若n为正整数,猜想13+23+33+…+n3的值;
(2)利用上题的结论比较13+23+33+…+1003与50002的大小.
【答案】解:(1)根据所给的数据可得:
13+23+33+…+n3=![]() .
.
故答案为:![]() .
.
(2)13+23+33+…+1003=![]()
=![]()
=50502>50002 ,
则13+23+33+…+1003>50002 .
【解析】(1)根据所给的数据,找出变化规律,即是![]() 乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案;
乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案;
(2)根据(1)所得出的规律,算出13+23+33+…+1003的结果,再与50002进行比较,即可得出答案.
【考点精析】认真审题,首先需要了解有理数的乘方(有理数乘方的法则:1、正数的任何次幂都是正数2、负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-an或(a -b)n=-(b-a)n , 当n为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,AB=![]() CD=
CD=![]() m,BC=3
m,BC=3![]() m,试求这块空地的面积.
m,试求这块空地的面积.
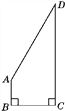
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,MA1∥NA2 , 则∠A1+∠A2= 度.
如图2,MA1∥NA3 , 则∠A1+∠A2+∠A3= 度.
如图3,MA1∥NA4 , 则∠A1+∠A2+∠A3+∠A4= 度.
如图4,MA1∥NA5 , 则∠A1+∠A2+∠A3+∠A4+∠A5= 度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn , 则∠A1+∠A2+∠A3+…+∠An= 度.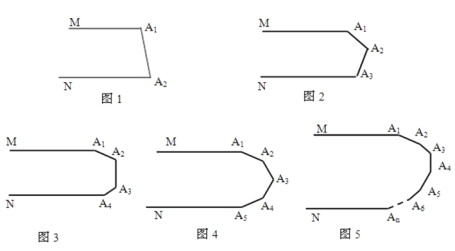
查看答案和解析>>
科目:初中数学 来源: 题型:
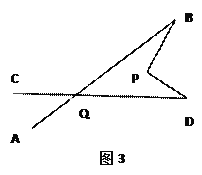
【题目】平面内的两条直线有相交和平行两种位置关系.
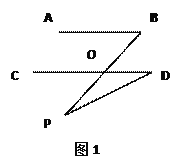
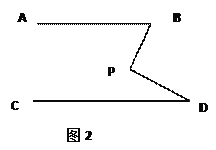
(1)AB∥CD.如图1,点P在AB,CD外部时,由AB∥CD,有∠B=∠BOD.又因为∠BOD是△POD的外角,故∠BOD=∠BPD +∠D ,得∠BPD=∠B-∠D.如图2,将点P移到AB,CD内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
(2)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?说明理由.
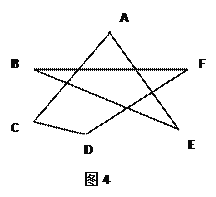
(3)根据(2)的结论,求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列作图语句正确的是( )
A. 作射线AB,使AB=a B. 作∠AOB=∠a
C. 延长直线AB到点C,使AC=BC D. 以点O为圆心作弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是严重缺水的国家之一,人均淡水资源为世界人均量的四分之一,所以我们要为中国节水,为世界节水.若每人每天浪费水0.32升,那么100万人每天浪费的水,用科学记数法表示为__________升.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
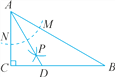
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com