
【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
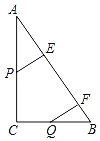
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
【答案】(1)4;(2)当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等;(3)当v=![]() cm/s时.t=
cm/s时.t=![]() 时,△PAE与△QBF全等.
时,△PAE与△QBF全等.
【解析】
(1)根据三角形的中线分三角形面积相等的两部分,可得当AP=PC时,直线BP平分△ABC的面积由此即可解决问题.
(2) 假设可能相等,利用勾股定理构建方程即可解决问题.
(3)分两种情形: ①当点Q在线段BC上时,PA=BQ时,△AEP≌△FQB, ②当P,Q在AC边上相遇时,且PA=PB时, △PAE与△QBF全等.分别求解即可解决问题.
解:(1)当AP=PC时,直线BP平分△ABC的面积.此时t=4.
故答案为4.
(2)假设可能相等.则有82+(6﹣t)2=62+(8﹣t)2,
解得t=0,不符合题意,
所以当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等.
(3)①当点Q在线段BC上时,
在Rt△AEP和Rt△BFQ中,
∵∠AEP=∠BFQ=90°,∠C=90°,
∴∠A+∠B=90°,∠B+∠BQF=90°,
∴∠A=∠BQF,
∴当PA=BQ时,△AEP≌△FQB,
∴当v=1cm/s时,0<t≤6时,△PAE与△QBF全等.
②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等.设此时PA=PB=x,
在Rt△PBC中,∵PB2=PC2+BC2,
∴x2=(8﹣x)2+62,
![]()
![]()
![]()
∵当P,Q在AC边上相遇,可得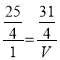
解得![]()
∴当v=![]() cm/s时.t=
cm/s时.t=![]() 时,△PAE与△QBF全等.
时,△PAE与△QBF全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
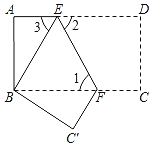
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=55°,求∠2、∠3的度数;
(3)若AB=6,AD=12,求△BC′F的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
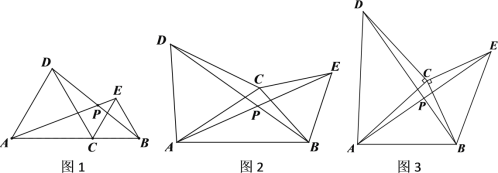
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC=30°,点D在射线BC上,且到A点的距离等于线段a的长.
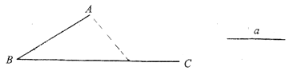
(1)用圆规和直尺在图中作出点D:(不写作法,但须保留作图痕迹,且说明结果
(2)如果AB=8,a=5.求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
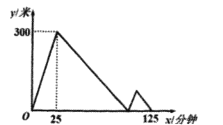
【题目】“龟、蟹赛跑趣事”:某天,乌龟和螃蟹在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑500米。当螃蟹领先乌龟300米时,螃蟹停下来休息并睡着了,当乌龟追上螃蟹的瞬间,螃蟹惊醒了(惊醒时间忽略不计)并立即以原来的速度继续跑向终点,并赢得了比赛。在比赛的整个过程中,乌龟和螃蟹的距离![]() (米)与乌龟出发的时间
(米)与乌龟出发的时间![]() (分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
(分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com