
【题目】如图,△ABC中,AC=4,BC=3,AB=5,AD为△ABC的角平分线,则CD的长度为( )

A.1B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过D作DP⊥AP于P,根据角平分线的性质可知∠CAD=∠BAD,利用AAS定理可知△ACD≌△APD.在在Rt△ABC中根据勾股定理得出AB的长,设DP=x,则DP=x,BD=3-x,在Rt△DPB中,利用勾股定理即可得出结论.
解:∵AC=4,BC=3,AB=5,
∴BC2+AC2=32+42=52=AB2,
∴∠C=90°,
过D作DP⊥AP于P,
∵AD平分∠BAC,
∴∠CAD=∠BAD.
又∵DC⊥AC、DP⊥AB,
∴∠C=∠APD.
在△ACD与APD中,
∵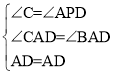
∴△ACD≌APD(AAS),
∴AP=AC=4,CD=PD,
设DP=x,则CP=x,BD=3﹣x,
在Rt△DPB中,∠DPB=90°,
∴DP2+PB2=DB2,
即x2+12=(3﹣x)2,
解得![]()
∴![]()
故选:D.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A(- 1,5),B(- 1,0),C(- 4,3).
中,A(- 1,5),B(- 1,0),C(- 4,3).

(1)求出△ABC的面积;
(2)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1;
轴的对称图形△A1B1C1;
(3)设P是y轴上的点,要使得点P到点A,C的距离和最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大丰区在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗5棵,B种树苗10棵,需要1300元;购买A种树苗3棵,B种树苗5棵,需要710元.
(1)求购买A,B两种树苗每棵各需要多少元?
(2)现需购进这两种树苗共100棵,其中A种树苗购进x棵,考虑到绿化效果和资金周转,A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过8650元,试求x 的取值范围。
(3)某包工队承包了该项种植任务,若种好一棵A种树苗需付工钱15元,种好一棵B种树苗需付工钱25元,在(2)的条件下,设种好这100棵树苗共需付工钱y元,,试求出y与x的函数表达式,并写出所付的种植工钱最少的购买方案及最少工钱是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
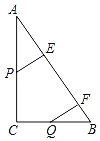
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
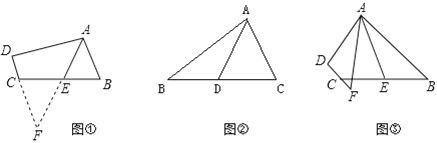
【题目】(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB,AD,DC之间的等量关系______.
(2)同题探究.
①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com