
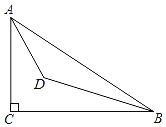
【题目】如图,∠C=90°,AC=3,BC=4,∠ABC和∠BAC的角平分线的交点是点D,则△ABD的面积为_____.
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
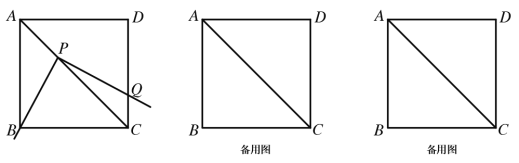
【题目】将一把三角尺放在边长为2的正方形ABCD上(正方形四个内角为90°,四边都相等),并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC交于点Q。
探究:(1)当点Q在边CD 上时,线段PQ 与线段PB之间有怎样的大小关系?试证明你观察得到结论;
(2)当点Q在边CD 上时,如果四边形 PBCQ 的面积为1,求AP长度;
(3)当点P在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q的位置,并求出相应的AP的长;如果不可能,试说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
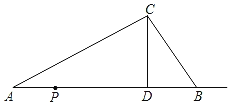
【题目】如图,△ABC中,CD为AB边上的高,AD=8,CD=4,BD=3.动点P从点A出发,沿射线AB运动,速度为1个单位/秒,运动时间为t秒.
(1)当t为何值时,△PDC≌△BDC;
(2)当t为何值时,△PBC是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
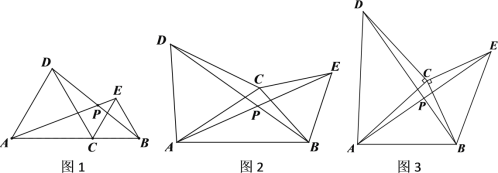
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是( )
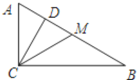
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向右跳动2个单位至点
,紧接着第2次向右跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点
,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点![]() 第2019次跳动至点
第2019次跳动至点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com