
【题目】如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 4
D. 4
【答案】B
【解析】
连接DO并延长交⊙O于E,连接BE,由DE是⊙O的直径,可得∠EBD=90°,由圆周角定理可得∠BED=∠BAD=60°,继而得∠BDE=30°,可求得BD、DE长,进而可得OA=OD=2![]() ,根据相似三角形的判定可得△OPD∽△BED,从而可得∠POD=∠EBD=90°,再根据勾股定理即可求得结论.
,根据相似三角形的判定可得△OPD∽△BED,从而可得∠POD=∠EBD=90°,再根据勾股定理即可求得结论.
连接DO并延长交⊙O于E,连接BE,
∵DE是⊙O的直径,
∴∠EBD=90°,
∵∠BED=∠BAD=60°,
∴∠EDB=30°,
∴DE=2BE,
∵PB=2,PD=6,
∴BD=6,
∵BD2+BE2=DE2,
∴DE=4![]() ,BE=2
,BE=2![]() ,
,
∴OA=OD==2![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠ODP=∠BDE,
∴△ODP∽△BDE,
∴∠POD=∠EBD=90°,
∴AD=![]() ,
,
故选B.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
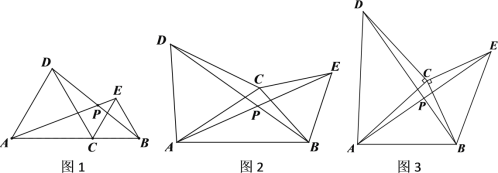
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是( )
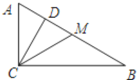
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC=30°,点D在射线BC上,且到A点的距离等于线段a的长.
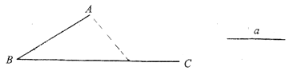
(1)用圆规和直尺在图中作出点D:(不写作法,但须保留作图痕迹,且说明结果
(2)如果AB=8,a=5.求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点C开始沿边CB向终点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,当点Q运动到点B时,两点停止运动.设运动时间为t秒.

(1)填空:BQ=______________cm,PB=_______________cm(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于![]() cm?
cm?
(3)是否存在t的值,使得五边形APQCD的面积等于27![]() ?若存在,请求出此时t的值;若不存在,请说明理由
?若存在,请求出此时t的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com