
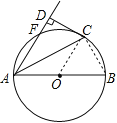
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】 (2)4
【解析】
试题(1)连结OC,由![]() =
=![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由![]() =
=![]() =
=![]() ,得∠BOC=60°,则∠BAC=30°,所以
,得∠BOC=60°,则∠BAC=30°,所以
∠DAC=30°,在Rt△ADC中,利用含30°的直角三角形三边的关系得AC=2CD=4![]() ,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=
,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=![]() AC=4,AB=2BC=8,所以⊙O的半径为4.
AC=4,AB=2BC=8,所以⊙O的半径为4.
试题解析:(1)证明:连结OC,如图,
∵![]() =
=![]()
∴∠FAC=∠BAC
∵OA=OC
∴∠OAC=∠OCA
∴∠FAC=∠OCA
∴OC∥AF
∵CD⊥AF
∴OC⊥CD
∴CD是⊙O的切线
(2)解:连结BC,如图
∵AB为直径
∴∠ACB=90°
∵![]() =
=![]() =
=![]()
∴∠BOC=![]() ×180°=60°
×180°=60°
∴∠BAC=30°
∴∠DAC=30°
在Rt△ADC中,CD=2![]()
∴AC=2CD=4![]()
在Rt△ACB中,BC=![]() AC=
AC=![]() ×4
×4![]() =4
=4
∴AB=2BC=8
∴⊙O的半径为4.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】函数![]() 、
、![]() 、
、![]() 都是常数,且
都是常数,且![]() 叫做“奇特函数”,当
叫做“奇特函数”,当![]() 时,奇特函数
时,奇特函数![]() 就成为反比例函数
就成为反比例函数![]() 是常数,且
是常数,且![]() .
.
![]() 若矩形的两边长分别是
若矩形的两边长分别是![]() 、
、![]() ,当两边长分别增加
,当两边长分别增加![]() 、
、![]() 后得到的新矩形的面积是
后得到的新矩形的面积是![]() ,求
,求![]() 与
与![]() 的函数关系式,并判断这个函数是否“奇特函数”;
的函数关系式,并判断这个函数是否“奇特函数”;
![]() 如图在直角坐标系中,点
如图在直角坐标系中,点![]() 为原点矩形
为原点矩形![]() 的顶点,
的顶点,![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() 、
、![]() 交于
交于![]() ,“奇特函数”
,“奇特函数”![]() 的图象经过点
的图象经过点![]() 、
、![]() ,求这个函数的解析式,并判断
,求这个函数的解析式,并判断![]() 、
、![]() 、
、![]() 三点是否在这个函数图象上;
三点是否在这个函数图象上;
![]() 对于
对于![]() 中的“奇特函数”
中的“奇特函数”![]() 的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.
的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
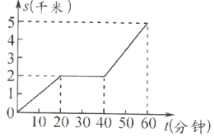
【题目】甲、乙两人同时从A地前往相距5千米的B地.甲骑自行车,途中修车耽误了20分钟,甲行驶的路程![]() (千米)关于时间
(千米)关于时间![]() (分钟)的函数图像如图所示;乙慢跑所行的路程
(分钟)的函数图像如图所示;乙慢跑所行的路程![]() (千米)关于时间
(千米)关于时间![]() (分钟)的函数解析式为
(分钟)的函数解析式为![]() .
.
(1)在图中画出乙慢跑所行的路程关于时间的函数图像;
(2)乙慢跑的速度是每分钟________千米;
(3)甲修车后行驶的速度是每分钟________千米;
(4)甲、乙两人在出发后,中途________分钟时相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A(- 1,5),B(- 1,0),C(- 4,3).
中,A(- 1,5),B(- 1,0),C(- 4,3).

(1)求出△ABC的面积;
(2)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1;
轴的对称图形△A1B1C1;
(3)设P是y轴上的点,要使得点P到点A,C的距离和最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com