
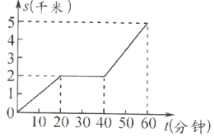
【题目】甲、乙两人同时从A地前往相距5千米的B地.甲骑自行车,途中修车耽误了20分钟,甲行驶的路程![]() (千米)关于时间
(千米)关于时间![]() (分钟)的函数图像如图所示;乙慢跑所行的路程
(分钟)的函数图像如图所示;乙慢跑所行的路程![]() (千米)关于时间
(千米)关于时间![]() (分钟)的函数解析式为
(分钟)的函数解析式为![]() .
.
(1)在图中画出乙慢跑所行的路程关于时间的函数图像;
(2)乙慢跑的速度是每分钟________千米;
(3)甲修车后行驶的速度是每分钟________千米;
(4)甲、乙两人在出发后,中途________分钟时相遇.
【答案】(1)图像见解析;(2)![]() ;(3)
;(3)![]() ;(4)24.
;(4)24.
【解析】
(1)根据所给解析式可知函数过原点,并过点(60,5),由这两点即可得出答案.
(2)乙慢跑的速度即是乙慢跑所行的路程s(千米)关于时间t(分钟)的函数解析式的斜率;
(3)甲修车后行驶路程是3km,所用时间是20min,即可求出速度;
(4)甲乙相遇,体现在(1)中的图形即是它们的交点,即求出交点得出答案.
(1)所画图形如下所示:
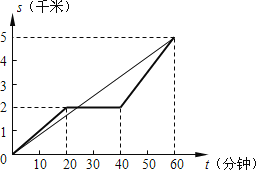
(2)乙慢跑的速度为:![]() 千米/分钟;
千米/分钟;
(3)甲修车后行驶20min,所形路程为3km,
故甲修车后行驶的速度为:3÷20=![]() km/min;
km/min;
(4)由甲行驶的路程s(千米)关于时间t(分钟)的函数图象与乙慢跑所行的路程s(千米)关于时间t(分钟)的函数图象可知:
在距离A地2km处甲乙相遇,此时乙行驶了2×12=24分钟,
即甲、乙两人在出发后,中途24分钟时相遇.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
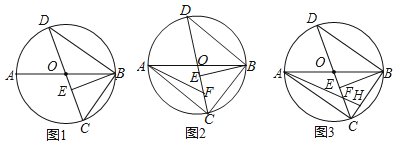
【题目】如图,AB、CD是![]() 的直径,
的直径,![]() 于E,连接BD.
于E,连接BD.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,F是OC上一点,
如图2,F是OC上一点,![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,连接BC,AF的延长线交BC于H,若
的条件下,连接BC,AF的延长线交BC于H,若![]() ,
,![]() ,求HF的长.
,求HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4cm,BC=8cm,动点P从点A出发,以1cm/s的速度沿AB向点B运动,动点Q从点B出发,以2cm/s秒的速度沿BC向点C运动.P、Q分别从A、B同时出发,设运动时间为t秒.(如图1)

(1)用含t的代数式表示下列线段长度:
①PB=__________cm,②QB=_____cm,③CQ=_________cm.
(2)当△PBQ的面积等于3![]() 时,求t的值.
时,求t的值.
(3) (如图2),若E为边CD中点,连结EQ、AQ.当以A、B、Q为顶点的三角形与△EQC相似时,直接写出满足条件的t的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程![]() 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com