【题目】一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行40米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，求这条河的宽度．（参考数值：tan31°≈ ）

参考答案：

【答案】解：过点C作CD⊥AB于D，

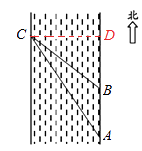
由题意∠DAC=31°，∠DBC=45°，

设CD=BD=x米，

则AD=AB+BD=（40+x）米，

在Rt△ACD中，tan∠DAC= ，

则 ，

解得x=60（米），

经检验得：x=60是原方程的根，

∴这条河的宽度为60米


【解析】根据已知添加辅助线过点C作CD⊥AB于D，构造Rt△CBD和Rt△CAD，根据题意可知CD=BD=x，然后在Rt△CAD，利用解直角三角形，建立关于x的方程，求解即可。
【考点精析】利用解直角三角形和关于方向角问题对题目进行判断即可得到答案，需要熟知解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)；指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角．

关闭