
【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

【答案】(1)60°;(2)30°;(3)不变.
【解析】
(1)由AM∥BN可得∠ABN=180°-∠A,再由BC、BD均为角平分线可求解;
(2)由AM∥BN可得∠ACB=∠CBN,再由∠ACB=∠ABD可得∠ABC =∠DBN;
(3)由AM∥BN可得∠APB=∠PBN,再由BD为角平分线即可解答.
解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=![]() (∠ABP+∠PBN)=
(∠ABP+∠PBN)=![]() ∠ABN=60°,
∠ABN=60°,
故答案为:60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=![]() ∠ABN=30°,
∠ABN=30°,
故答案为:30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=![]() ∠PBN=
∠PBN=![]() ∠APB,即∠APB:∠ADB=2:1.
∠APB,即∠APB:∠ADB=2:1.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
A.5米
B.7米
C.7.5米
D.21米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如上图,在正方形网格上有△A1B1C1和△A2B2C2 , 这两个三角形是否相似?”,那么你认为△A1B1C1和△A2B2C2 , (相似或不相似);理由是 . 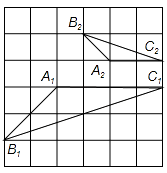
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com