
【题目】(1)如图1所示,在△ABC中,若AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E.AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN,试判断△AMN的形状,并证明你的结论.
(2)如图2所示,在△ABC中,若∠C=45°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN,若AC=3![]() ,BC=8,求MN的长.
,BC=8,求MN的长.

【答案】(1)详见解析;(2)MN=1.6
【解析】
(1)由AB=AC,可得∠B=∠C=30°,又由AB的垂直平分线EM交BC于M,得出∠BAM=30°,即可得出∠AMN=60°,同理:∠ANM=60°,即可得出结论;
(2)先利用NF是AC垂直平分线计算出CN,进而得出AN,进而得出BM=6-MN,最后用勾股定理即可得出结论.
(1)∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,
∵AB的垂直平分线交BC于点M, ∴AM=BM,
∴∠BAM=∠ABM=30°,∴∠AMN=∠ABM+∠BAM=60°,
同理:∠ANM=60°,∴△AMN是等边三角形;
(2)∵NF是AC的垂直平分线,
∴∠ANC=2∠CNF,CF=![]() ,AN=CN,
,AN=CN,
在Rt△CFN中,∠C=45°,∴∠CNF=∠C=45°,CN=![]() =3,
=3,
∴∠ANC=90°,AN=3,∵BC=8,
∴BN=BC﹣CN=5=BM +MN,∴BM=5﹣MN,
∵ME是AB的垂直平分线,∴AM=BM=5﹣MN,
在Rt△AMN中,根据勾股定理得,(5﹣MN)2﹣MN2=9,∴MN=1.6


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
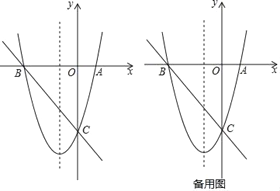
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递员开摩托车从总部A点出发,在一条南北公路上来回收取包裹,现在记录下他连续行驶的情况(以向南为正方向,单位:千米):5,2,-4,![]() ,3,-2.5,6.请问
,3,-2.5,6.请问
(1)他最后一次收取包裹后在出发点A的什么位置?
(2)如果摩托车每千米耗油30毫升,出发前摩托车有油1000毫升,快递员在收完包裹后能回到总部吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2
B、4
C、![]()
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察数轴,请回答:
![]()
(1)点![]() 与点
与点![]() 的距离为 ,点
的距离为 ,点![]() 与点
与点![]() 的距离为 ;
的距离为 ;
点![]() 与点
与点![]() 的距离为 ,点
的距离为 ,点![]() 与点
与点![]() 的距离为 ;
的距离为 ;
(2)发现:在数轴上,如果点![]() 与点
与点![]() 分别表示数
分别表示数![]() ,则它们之间的距离可表示为
,则它们之间的距离可表示为![]() (用
(用![]() 表示);
表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示![]() 的点
的点![]() 与
与![]() 之间的距离是
之间的距离是![]() ,则
,则![]() 的值是 ;
的值是 ;
②![]() ,则
,则![]() ;
;
③数轴上是否存在表示![]() 的点
的点![]() ,使点
,使点![]() 到点
到点![]() 、点
、点![]() 的距离之和为
的距离之和为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
④![]() 的最小值为 ;
的最小值为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.数据收集整理后,绘制了图1和图2两幅不完整的统计图,请根据统计图中的信息解答下列问题:
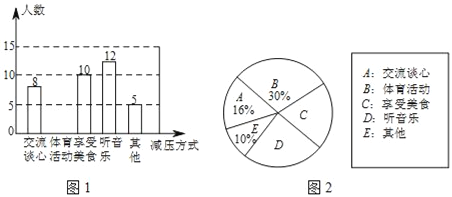
(1)请通过计算,补全条形统计图;
(2)请直接写出扇形统计图中“享受美食”所对应圆心角的度数为 ;
(3)根据调查结果,可估计出该校九年级学生中减压方式的众数和中位数分别是 , .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com