
����Ŀ����ͼ����֪������y=![]() x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
��1����ֱ��BC�Ľ���ʽ��
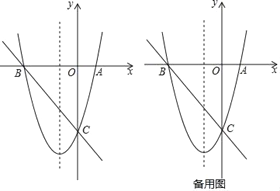
��2����F��ֱ��BC�·��������ϵ�һ�㣬����BCF��������ʱ���������ߵĶԳ�������һ��P��ʹ����BFP���ܳ���С���������F������͵�P�����ꣻ
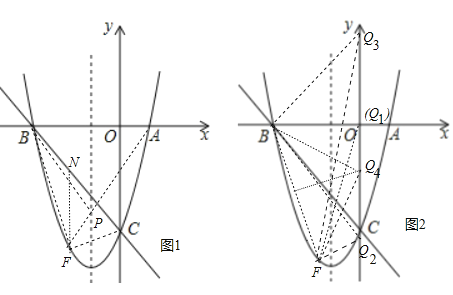
��3���ڣ�2���������£��Ƿ���������ĵ�Q��0��m����ʹ����BFQΪ���������Σ�����У���ֱ��д����Q�����ꣻ���û�У���˵�����ɣ�
���𰸡���1��y=��x��8����2��F����4����12����P����3����10������3��������.
�������������������1�����ô���ϵ�������B��C�������꼴�ɽ��������
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
��3����ͼ2������������������������FQ1=FBʱ��Q1��0��0��������BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
���������������1������������y=![]() x2+3x��8����y=0���õ���
x2+3x��8����y=0���õ��� ![]() x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b��������
x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b�������� ![]() �������
������� ![]() ����ֱ��BC�Ľ���ʽΪy=��x��8��
����ֱ��BC�Ľ���ʽΪy=��x��8��
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8��
m2+3m��8������N��m����m��8��
��S��FBC=S��FNB+S��FNC=![]() FN��8=4FN=4[����m��8������
FN��8=4FN=4[����m��8������![]() m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3����B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С����ֱ��AF�Ľ���ʽΪy=ax+b��������
m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3����B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С����ֱ��AF�Ľ���ʽΪy=ax+b�������� ![]() �������
������� ![]() ����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
��3����ͼ2�У���B����8��0����F����4��0������BF=![]() =
=![]() �����������������
�����������������
����FQ1=FBʱ��Q1��0��0����
����BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ����
����
����Q4B=Q4Fʱ����Q4��0��m��������82+m2=42+��m+12��2�����m=��4����Q4��0����4��
��Q��������0��0����0�� ![]() ����0����
����0����![]() ����0����4����
����0����4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֲ�����
��1����ͼ1����һ��ֱ�����ǰ�DEF������ֱ�����ǰ�ABC�ϣ�ʹ���ǰ�DEF������ֱ�DZ�DE��DF�ֱ���B��C����BC��EF����֪��A=30�㣬���ABD+��ACD= �ȣ�
��2����ͼ2����BDC���A����B����C֮�������ʲô��ϵ����˵�����ɣ�
��3�����Ӧ�ã�����ֱ���������Ͻ��ۣ�������������⣺��ͼ3��BEƽ�֡�ABD��CEƽ�֡�ACD������BAC=40�㣬��BDC=120�㣬���BEC�Ķ�����



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��������Ƶ�ʹ��Ƹ�����������ʱ��ͳ����ijһ������ֵ�Ƶ�ʣ���������ͼ��ʾ������ͳ��ͼ���������һ������������п��ܵ���(����)

A. ����ʯͷ����������������Ϸ����С�������������������
B. һ��ȥ����С������ͨ�˿���ϴ�Ⱥ��������γ�һ���ƵĻ�ɫ�Ǻ���
C. ��������1�������2������������ֻ����ɫ�ϵ�������������ȡһ���ǻ���
D. ��һ���ʵؾ��ȵ������������������ϵ��������4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��6��ͬѧ������(��λ��cm)������±���
ͬѧ | A | B | C | D | E | F |
���� | 165 | 166 | 171 | |||
������༶ƽ�����ߵIJ�ֵ | ��1 | ��2 | ��3 | ��3 |
(1)��ɱ��пհIJ��֣�
(2)���ǵ��������������������٣�
(3)����6�˵�ƽ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC����һ��D��AD=5��BD=6��CD=4������ABD��A����ʱ����ת��ʹAB��AC�غϣ���D��ת����E��
��1��DE=_____��
��2����CDE������ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O����DE��AC��CE��BD��
��1����֤���ı���OCED�����Σ�
��2������BAC=30�㣬AC=4��������OCED�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ֽ�һ�����ֱ�����ǰ�ABC���ڵ�һ���ޣ�б���������������ϣ��ҵ�A��0��2������C��1��0����BE��x���ڵ�E��һ�κ���y=x+b������B����y���ڵ�D��
��1����֤����AOC�ա�CEB��
��2�����ABD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ƴ��������������ƣ�ÿ����ȡ����y��Ԫ��������ʱ��x��Сʱ���ĺ�����ϵ��ͼ��ʾ������BA���߶Σ���BA��x�ᣬAC�����ߣ�
��1����x��30����y��x֮��ĺ�����ϵʽ��
��2����С��4�·�����20Сʱ����Ӧ������Ԫ���������ã�
��3����С��5�·���������Ϊ75Ԫ�������ڸ��·ݵ�����ʱ���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1��ʾ���ڡ�ABC�У���AB��AC����BAC��120�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�M����AB�ڵ�E��AC�Ĵ�ֱƽ���߽�BC�ڵ�N����AC�ڵ�F������AM��AN�����жϡ�AMN����״����֤����Ľ��ۣ�
��2����ͼ2��ʾ���ڡ�ABC�У�����C��45�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�M����AB�ڵ�E��AC�Ĵ�ֱƽ���߽�BC�ڵ�N����AC�ڵ�F������AM��AN����AC��3![]() ��BC��8����MN�ij���
��BC��8����MN�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com